Variational Inference in Python¶
PyData DC 2016¶
October 8, 2016¶
@AustinRochford — Monetate Labs
arochford@monetate.com¶
Bayesian Inference¶
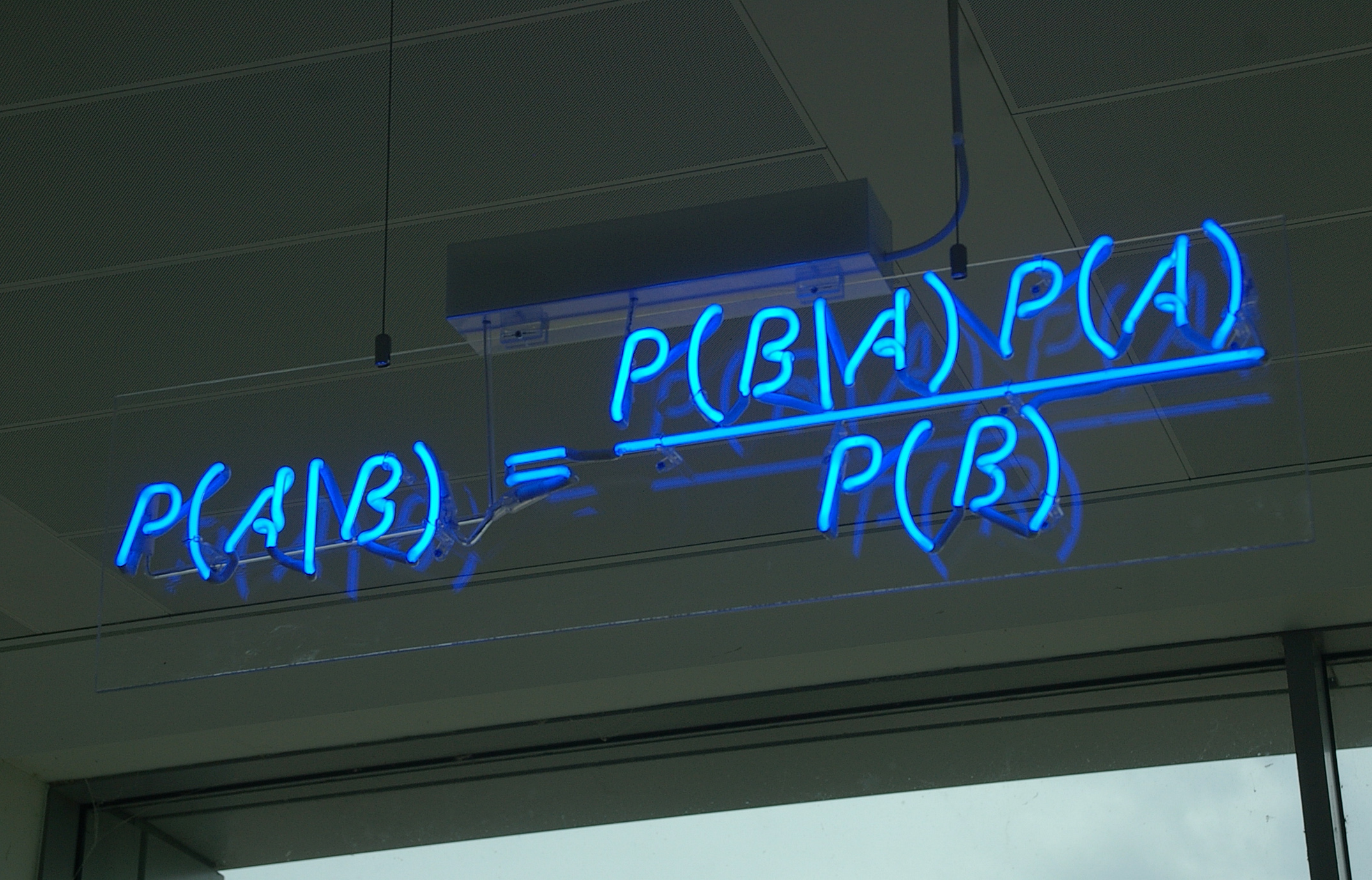
The posterior distribution is equal to the joint distribution divided by the marginal distribution of the evidence.
$$ \color{red}{P(\theta\ |\ \mathcal{D})} = \frac{\color{blue}{P(\mathcal{D}\ |\ \theta)\ P(\theta)}}{\color{green}{P(\mathcal{D})}} = \frac{\color{blue}{P(\mathcal{D}, \theta)}}{\color{green}{\int P(\mathcal{D}\ |\ \theta)\ P(\theta)\ d\theta}} $$For many useful models the marginal distribution of the evidence is hard or impossible to calculate analytically.
Modes of Bayesian Inference¶
- Conjugate models with closed-form posteriors
- Markov chain Monte Carlo algorithms
- Approximate Bayesian computation
- Distributional approximations
- Laplace approximations, INLA
- Variational inference
Markov Chain Monte Carlo Algorithms¶
- Construct a Markov chain whose stationary distribution is the posterior distribution
- Sample from the Markov chain for a long time
- Approximate posterior quantities using the empirical distribution of the samples
HTML(mcmc_video)
Beta-Binomial Model¶
We observe three successes in ten trials, and want to infer the true success probability.
x_beta_binomial = np.array([1, 1, 1, 0, 0, 0, 0, 0, 0, 0])
import pymc3 as pm
with pm.Model() as beta_binomial_model:
p_beta_binomial = pm.Uniform('p', 0., 1.)
Applied interval-transform to p and added transformed p_interval_ to model.
with beta_binomial_model:
x_obs = pm.Bernoulli('y', p_beta_binomial,
observed=x_beta_binomial)
fig
with beta_binomial_model:
beta_binomial_trace_ = pm.sample(BETA_BINOMIAL_SAMPLES, random_seed=SEED)
beta_binomial_trace = beta_binomial_trace_[BETA_BINOMIAL_BURN::BETA_BINOMIAL_THIN]
Assigned NUTS to p_interval_ [-------100%-------] 50000 of 50000 in 13.1 sec. | SPS: 3829.8 | ETA: 0.0
fig
Pros¶
- Asymptotically unbiased: converges to the true posterior afer many samples
- Model-agnostic algorithms
- Well-studied for more than 60 years
Cons¶
- Can take a long time to converge
- Can be difficult to assess convergence
- Difficult to scale
Variational Inference¶
- Choose a class of approximating distributions
- Find the best approximation to the true posterior
Variational inference minimizes the Kullback-Leibler divergence
$$\mathbb{KL}(\color{purple}{q(\theta)} \parallel \color{red}{p(\theta\ |\ \mathcal{D})}) = \mathbb{E}_q\left(\log\left(\frac{\color{purple}{q(\theta)}}{\color{red}{p(\theta\ |\ \mathcal{D})}}\right)\right)$$from approximate distributons, but we can't calculate the true posterior distribution.
Minimizing the Kullback-Leibler divergence
$$ \mathbb{KL}(\color{purple}{q(\theta)} \parallel \color{red}{p(\theta\ |\ \mathcal{D})}) = -(\underbrace{\mathbb{E}_q(\log \color{blue}{p(\mathcal{D}, \theta))} - \mathbb{E}_q(\color{purple}{\log q(\theta)})}_{\color{orange}{\textrm{ELBO}}}) + \log \color{green}{p(\mathcal{D})} $$is equivalent to maximizing the Evidence Lower BOund (ELBO), which only requires calculating the joint distribution.
Variational Inference Example¶
fig
Approximate the true distribution using a diagonal covariance Gaussian from the class
$$\mathcal{Q} = \left\{\left.N\left(\begin{pmatrix} \mu_x \\ \mu_y \end{pmatrix}, \begin{pmatrix} \sigma_x^2 & 0 \\ 0 & \sigma_y^2\end{pmatrix}\ \right|\ \mu_x, \mu_y \in \mathbb{R}^2, \sigma_x, \sigma_y > 0\right)\right\}$$fig
Pros¶
- A principled method to trade complexity for bias
- Optimization theory is applicable
- Assesment of convergence
- Scalability
Cons¶
- Biased estimate of the true posterior
- Better for prediction than interpretation
- Model-specific algorithms
Mean field variational inference¶
Assume the variational distribution factors independently as $q(\theta_1, \ldots, \theta_n) = q(\theta_1) \cdots q(\theta_n)$
The variational approximation can be found by coordinate ascent
$$ \begin{align*} q(\theta_i) & \propto \exp\left(\mathbb{E}_{q_{-i}}(\log(\mathcal{D}, \boldsymbol{\theta}))\right) \\ q_{-i}(\boldsymbol{\theta}) & = q(\theta_1) \cdots q(\theta_{i - 1})\ q(\theta_{i + 1}) \cdots q(\theta_n) \end{align*} $$Coordinate Ascent Cons¶
- Calculations are tedious, even when possible
- Convergence is slow when the number of parameters is large
Automating Variational Inference in Python¶
- Maximize ELBO using gradient ascent instead of coordinate ascent
- Tensor libraries calculate ELBO gradients automatically
Common themes¶
- Monte Carlo estimate of the ELBO gradient
- Minibatch estimates of the joint distribution
BBVI and ADVI arise from different ways of calculating the ELBO gradient
Beta-binomial model¶
import edward as ed
from edward.models import Bernoulli, Beta, Uniform
ed.set_seed(SEED)
# probability model
p = Uniform(a=0., b=1.)
x_edward_beta_binomial = Bernoulli(p=p)
data = {x_edward_beta_binomial: x_beta_binomial}
# variational approximation
q_p = Beta(a=tf_positive_variable(),
b=tf_positive_variable())
q = {p: q_p}
%%time
beta_binomial_inference = ed.MFVI(q, data)
beta_binomial_inference.run(n_iter=10000, n_print=None)
CPU times: user 5.83 s, sys: 880 ms, total: 6.71 s Wall time: 4.63 s
fig
from edward.models import PyMC3Model
# probability model
x_beta_binomial_obs = shared(np.zeros(1))
with pm.Model() as beta_binomial_model_untransformed:
p = pm.Uniform('p', 0., 1., transform=None)
x_beta_binomial_ = pm.Bernoulli('x', p, observed=x_beta_binomial_obs)
pymc3_data = {x_beta_binomial_obs: x_beta_binomial}
pymc3_beta_binomial_model = PyMC3Model(beta_binomial_model_untransformed)
%%time
# variational distribution
pymc3_q_p = Beta(a=tf_positive_variable(),
b=tf_positive_variable())
pymc3_q = {'p': pymc3_q_p}
pymc3_beta_binomial_inference = ed.MFVI(pymc3_q, pymc3_data,
pymc3_beta_binomial_model)
pymc3_beta_binomial_inference.run(n_iter=30000, n_print=None)
CPU times: user 29.3 s, sys: 5.54 s, total: 34.8 s Wall time: 22.4 s
fig
Edward-supported modeling "languages"¶
Direction density calculations
|
Congressional Ideal Points¶
vote_df.head()
| party | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| rep | |||||||||||||||||
| 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | NaN | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | NaN |
| 2 | 1 | NaN | 1 | 1 | NaN | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 |
| 3 | 1 | 0 | 1 | 1 | 0 | NaN | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 |
| 4 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | NaN | 1 | 1 | 1 | 1 |
grid.fig
Idea:
- Representatives ($\color{blue}{\alpha_i}$) and bills ($\color{green}{\beta_j}$) each have an ideal point on a spectrum of conservativity
- If a representative's and bill's ideal points are the same, the representative has a 50% chance of voting for the bill
- Bills also have an ability to discriminate ($\color{red}{\gamma_j}$) between conservative and liberal representatives
- Some bills have broad bipartisan support, while some provoke votes along party lines
Representative ideal points¶
$$ \begin{align*} \color{blue}{\alpha_1}, \ldots, \color{blue}{\alpha_N} & \sim N(0, 1) \end{align*} $$def normal_log_prior(value, loc=0., scale=1.):
return tf.reduce_sum(normal.log_pdf(value, loc, scale))
Bill ideal points and discriminative abilities¶
$$ \begin{align*} \mu_{\beta} & \sim N(0, 1) \\ \sigma_{\beta} & \sim U(0, 1) \\ \color{green}{\beta_1}, \ldots, \color{green}{\beta_K} & \sim N(\mu_{\beta}, \sigma_{\beta}^2) \end{align*} $$
$$
\begin{align*}
\mu_{\gamma}
& \sim N(0, 1) \\
\sigma_{\gamma}
& \sim U(0, 1) \\
\color{red}{\gamma_1}, \ldots, \color{red}{\gamma_K}
& \sim N(\mu_{\gamma}, \sigma_{\gamma}^2)
\end{align*}
$$
def hierarchical_log_prior(value, mu, sigma):
log_hyperprior = normal_log_prior(mu) + uniform.log_pdf(sigma, 0., 1.)
return log_hyperprior + normal_log_prior(value, loc=mu, scale=sigma)
Observation model¶
$$ \begin{align*} \mathbb{P}(\textrm{Representative }i \textrm{ votes for bill }j\ |\ \color{blue}{\alpha_i}, \color{green}{\beta_j}, \color{red}{\gamma_j}) & = \frac{1}{1 + \exp(-\color{red}{\gamma_j} \left(\color{blue}{\alpha_i} - \color{green}{\beta_j}\right))} \end{align*} $$def log_like(vote, rep, bill, alpha, beta, gamma):
# alpha, beta, and gamma have one entry for representative/bill,
# index them to have one entry per representative/bill combination
alpha_long = long_from_indices(alpha, rep)
beta_long = long_from_indices(beta, bill)
gamma_long = long_from_indices(gamma, bill)
p = tf.sigmoid(gamma_long * (alpha_long - beta_long))
return tf.reduce_sum(bernoulli.logpmf(vote, p))
Edward model¶
class IdealPoint:
def log_prob(self, xs, zs):
"""
xs is a dictionary of observed data
zs is a dictionary of parameters
Calculates the model's log joint distribution
"""
# parameters
alpha, beta, gamma = zs['alpha'], zs['beta'], zs['gamma']
mu_beta, mu_gamma = zs['mu_beta'], zs['mu_gamma']
sigma_beta, sigma_gamma = zs['sigma_beta'], zs['sigma_gamma']
# observed data
vote, bill, rep = xs['vote'], xs['bill'], xs['rep']
# log joint distribution
log_prior_ = log_prior(alpha,
beta, mu_beta, sigma_beta,
gamma, mu_gamma, sigma_gamma)
log_like_ = log_like(vote, rep, bill,
alpha, beta, gamma)
return log_prior_ + log_like_
ideal_point_model = IdealPoint()
BBVI inference¶
# variational distribution
q_alpha = tf_normal((n_reps,))
q_mu_beta = tf_normal()
q_sigma_beta = tf_uniform()
q_beta = tf_normal((N_BILLS,))
q_mu_gamma = tf_normal()
q_sigma_gamma = tf_uniform()
q_gamma = tf_normal((N_BILLS,))
q = {
'alpha': q_alpha,
'beta': q_beta, 'mu_beta': q_mu_beta, 'sigma_beta': q_sigma_beta,
'gamma': q_gamma, 'mu_gamma': q_mu_gamma, 'sigma_gamma': q_sigma_gamma,
}
%%time
inference = ed.MFVI(q, ideal_point_data, ideal_point_model)
inference.run(n_iter=20000, n_print=None)
CPU times: user 1min 33s, sys: 30.2 s, total: 2min 4s Wall time: 52.8 s
fig
Fun project: Recreate the Martin-Quinn dynamic ideal point model for ideology of U.S. Supreme Court justices with Edward

Variational Inference with PyMC3¶
Automatic Differentiation Variational Inference (ADVI)¶
- Only applicable to differentiable probability models
- Transform constrained parameters to be unconstrained
- Approximate the posterior for unconstrained parameters with mean field Gaussian
Beta-binomial model¶
Transformed distributions¶
fig
%%time
with beta_binomial_model:
advi_fit = pm.advi(n=20000, random_seed=SEED)
Iteration 0 [0%]: ELBO = -10.91 Iteration 2000 [10%]: Average ELBO = -7.76 Iteration 4000 [20%]: Average ELBO = -7.37 Iteration 6000 [30%]: Average ELBO = -7.24 Iteration 8000 [40%]: Average ELBO = -7.22 Iteration 10000 [50%]: Average ELBO = -7.17 Iteration 12000 [60%]: Average ELBO = -7.15 Iteration 14000 [70%]: Average ELBO = -7.19 Iteration 16000 [80%]: Average ELBO = -7.18 Iteration 18000 [90%]: Average ELBO = -7.19 Finished [100%]: Average ELBO = -7.2 CPU times: user 3.12 s, sys: 0 ns, total: 3.12 s Wall time: 3.1 s
ADVI approxiation to transformed posterior¶
fig
ADVI approximation to posterior¶
fig
Dependent Density Regression¶
fig
Idea: A mixture of linear models, where the unknown number of mixture weights depend on $x$
fig
Mixture weights¶
The model has infinitely many mixture components, we truncate to $K$
$$ \begin{align*} \alpha_1, \ldots, \alpha_K & \sim N(0, 1) \\ \beta_1, \ldots, \beta_K & \sim N(0, 1) \\ \boldsymbol{\pi} \ |\ \boldsymbol{\alpha}, \boldsymbol{\beta}, x & \sim \textrm{Logit-Stick-Breaking}(\boldsymbol{\alpha} + \boldsymbol{\beta} x) \\ \end{align*} $$K = 20
x_lidar = shared(std_range, broadcastable=(False, True))
with pm.Model() as lidar_model:
alpha = pm.Normal('alpha', 0., 1., shape=K)
beta = pm.Normal('beta', 0., 1., shape=K)
v = tt.nnet.sigmoid(alpha + beta * x_lidar)
pi = pm.Deterministic('pi', stick_breaking(v))
Component linear models¶
$$ \begin{align*} \gamma_1, \ldots, \gamma_K & \sim N(0, 100) \\ \delta_1, \ldots, \delta_K & \sim N(0, 100) \\ \tau_1, \ldots, \tau_K & \sim \textrm{Gamma}(1, 1) \\ Y_i\ |\ \gamma_i, \delta_i, \tau_i, x & \sim N(\gamma_i + \delta_i x, \tau_i^{-1}) \end{align*} $$with lidar_model:
gamma = pm.Normal('gamma', 0., 100., shape=K)
delta = pm.Normal('delta', 0., 100., shape=K)
tau = pm.Gamma('tau', 1., 1., shape=K)
ys = pm.Deterministic('ys', gamma + delta * x_lidar)
Applied log-transform to tau and added transformed tau_log_ to model.
Observation model¶
$$ \begin{align*} Y\ |\ \boldsymbol{\alpha}, \boldsymbol{\beta}, \boldsymbol{\gamma}, \boldsymbol{\delta}, \boldsymbol{\tau}, x & = \sum_{i = 1}^K \pi_i Y_i \\ \end{align*} $$with lidar_model:
lidar_obs = NormalMixture('lidar_obs', pi, ys, tau,
observed=std_logratio)
ADVI inference¶
%%time
N_ADVI_ITER = 50000
with lidar_model:
advi_fit = pm.advi(n=N_ADVI_ITER, random_seed=SEED)
Iteration 0 [0%]: ELBO = -1173858.35 Iteration 5000 [10%]: Average ELBO = -1472209.86 Iteration 10000 [20%]: Average ELBO = -893902.97 Iteration 15000 [30%]: Average ELBO = -665586.63 Iteration 20000 [40%]: Average ELBO = -369517.75 Iteration 25000 [50%]: Average ELBO = 12058.54 Iteration 30000 [60%]: Average ELBO = 130100.63 Iteration 35000 [70%]: Average ELBO = 186668.28 Iteration 40000 [80%]: Average ELBO = 222983.67 Iteration 45000 [90%]: Average ELBO = 253507.05 Finished [100%]: Average ELBO = 266985.1 CPU times: user 43.7 s, sys: 0 ns, total: 43.7 s Wall time: 43.7 s
fig
Posterior predictions¶
PPC_SAMPLES = 5000
lidar_ppc_x = np.linspace(std_range.min() - 0.05,
std_range.max() + 0.05,
100)
with lidar_model:
# sample from the variational posterior distribution
advi_trace = pm.sample_vp(advi_fit, PPC_SAMPLES, random_seed=SEED)
# sample from the posterior predictive distribution
x_lidar.set_value(lidar_ppc_x[:, np.newaxis])
advi_ppc_trace = pm.sample_ppc(advi_trace, PPC_SAMPLES, random_seed=SEED)
Impact of truncation¶
fig
fig
References¶
Edward¶
PyMC3¶
http://pymc-devs.github.io/pymc3/
PyMC3 port of Probabilistic Programming and Bayesian Methods for Hackers
Variational Inference¶
Angelino, Elaine, Matthew James Johnson, and Ryan P. Adams. "Patterns of Scalable Bayesian Inference." arXiv preprint arXiv:1602.05221 (2016).
Blei, David M., Alp Kucukelbir, and Jon D. McAuliffe. "Variational inference: A review for statisticians." arXiv preprint arXiv:1601.00670 (2016).
Kucukelbir, Alp, et al. "Automatic Differentiation Variational Inference." arXiv preprint arXiv:1603.00788 (2016).
Ranganath, Rajesh, Sean Gerrish, and David M. Blei. "Black Box Variational Inference." AISTATS. 2014.
Models¶
Bafumi, Joseph, et al. "Practical issues in implementing and understanding Bayesian ideal point estimation." Political Analysis 13.2 (2005): 171-187.
Fox, Jean-Paul. Bayesian item response modeling: Theory and applications. Springer Science & Business Media, 2010.
Gelman, Andrew, et al. Bayesian data analysis. Vol. 2. Boca Raton, FL, USA: Chapman & Hall/CRC, 2014.
Gelman, Andrew, and Jennifer Hill. Data analysis using regression and multilevel/hierarchical models. Cambridge University Press, 2006.
Ren, Lu, et al. "Logistic stick-breaking process." Journal of Machine Learning Research 12.Jan (2011): 203-239.
Thank You!¶
@AustinRochford — Monetate Labs
arochford@monetate.com¶

The Jupyter notebook these slides were generated from is available here
