About Me¶

@AustinRochford • austinrochford.com • github.com/AustinRochford¶
austin.rochford@gmail.com • arochford@monetate.com¶
PyMC3 contributor • Principal Data Scientist at Monetate Labs¶
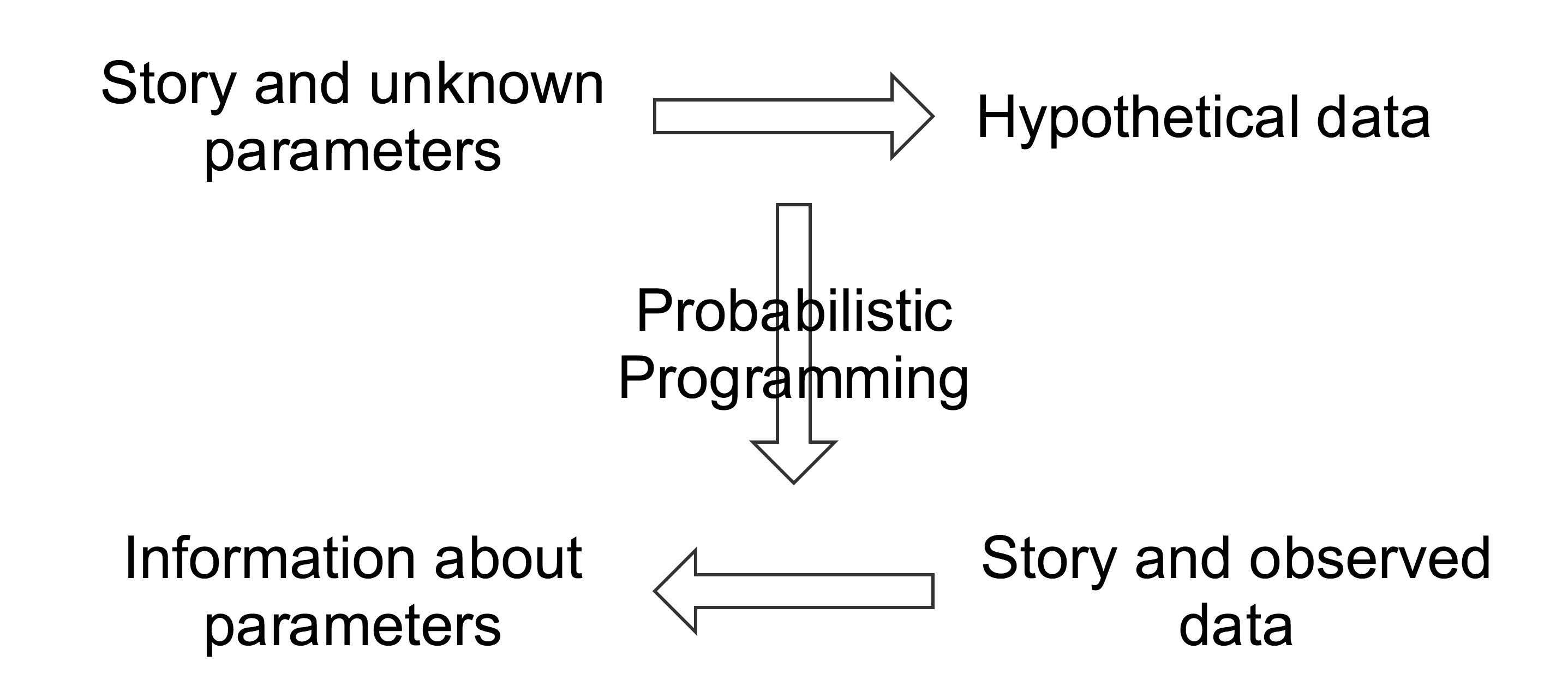
Probabilistic Programming¶
- Write a program to simulate the data generating process
- Language runtime/software library performs inference

Probabilistic Programming — storytelling enables inference
Enter: Bayes theorem¶
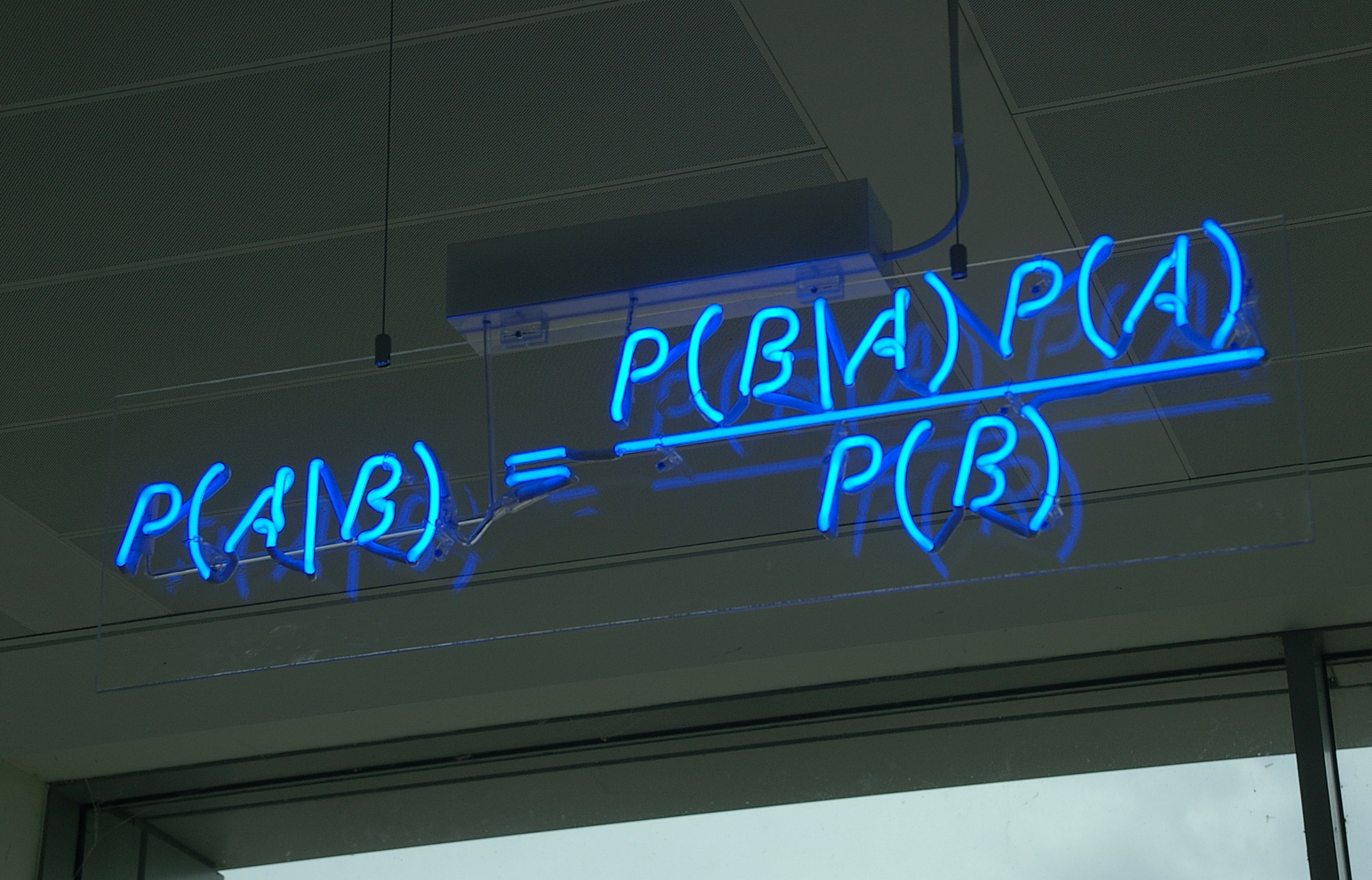
Benefits of probabilistic programming¶
- Model-agnostic inference algorithms
- Quantification of uncertainty
- Incorporation of domain knowledge
- Modularity
Initially, we have no information about which door the prize is behind.
import pymc3 as pm
with pm.Model() as monty_model:
prize = pm.DiscreteUniform('prize', 0, 2)
If we choose door one:
| Prize behind | Door 1 | Door 2 | Door 3 |
|---|---|---|---|
| Door 1 | No | Yes | Yes |
| Door 2 | No | No | Yes |
| Door 2 | No | Yes | No |
from theano import tensor as tt
with monty_model:
p_open = pm.Deterministic('p_open',
tt.switch(tt.eq(prize, 0),
# it is behind the first door
np.array([0., 0.5, 0.5]),
tt.switch(tt.eq(prize, 1),
# it is behind the second door
np.array([0., 0., 1.]),
# it is behind the third door
np.array([0., 1., 0.]))))
Monty opened the third door, revealing a goat.

with monty_model:
opened = pm.Categorical('opened', p_open, observed=2)
Should we switch our choice of door?
with monty_model:
monty_trace = pm.sample(1000, init=None, random_seed=SEED)
monty_df = pm.trace_to_dataframe(monty_trace)
Assigned Metropolis to prize 100%|██████████| 1000/1000 [00:00<00:00, 2850.75it/s]
monty_df.head()
| prize | p_open__0 | p_open__1 | p_open__2 | |
|---|---|---|---|---|
| 0 | 1 | 0.0 | 0.0 | 1.0 |
| 1 | 0 | 0.0 | 0.5 | 0.5 |
| 2 | 0 | 0.0 | 0.5 | 0.5 |
| 3 | 0 | 0.0 | 0.5 | 0.5 |
| 4 | 0 | 0.0 | 0.5 | 0.5 |
monty_df.prize.mean()
0.67300000000000004
fig

From the PyMC3 documentation:
PyMC3 is a Python package for Bayesian statistical modeling and Probabilistic Machine Learning which focuses on advanced Markov chain Monte Carlo and variational fitting algorithms. Its flexibility and extensibility make it applicable to a large suite of problems.
PyMC3 features¶
- Uses Theano as a computational backend
- Automated differentiation, dynamic C compilation, GPU integration
- Implements Hamiltonian Monte Carlo and No-U-Turn sampling
- High-level GLM (
R-like syntax) and Gaussian process specification - Provides a framework for operator variational inference
HTML(mcmc_video)
Statistical workflow¶
- Tell a story about how the data may have been generated
- Encode that story as a probabilistic model
- Perform inference
- Check model diagnostics
- Compare models
- Iterate (
GOTO 1)
Statistical LEGOs¶

Case study: NBA foul calls¶

Last two minute report¶
nba_df.head()
| seconds_left | review_decision | away | home | score_away | score_home | disadvantaged_team | committing_team | |
|---|---|---|---|---|---|---|---|---|
| 0 | 111.0 | INC | UTA | POR | 104.0 | 113.0 | POR | UTA |
| 1 | 102.0 | CNC | UTA | POR | 104.0 | 113.0 | UTA | POR |
| 2 | 98.0 | CC | UTA | POR | 104.0 | 113.0 | POR | UTA |
| 3 | 64.0 | CNC | UTA | POR | 104.0 | 113.0 | UTA | POR |
| 4 | 62.0 | INC | UTA | POR | 104.0 | 113.0 | POR | UTA |
Story¶
Close basketball games usually end with intentional fouls.
fig
Model¶
The foul call probability varies over time.
seconds_left_ = theano.shared(seconds_left)
with pm.Model() as nba_model:
β = pm.GaussianRandomWalk('β', tau=PRIOR_PREC, init=pm.Normal.dist(0., 10.),
shape=n_sec)
Transform logodds to probabilities, specify observation model.
with nba_model:
p = pm.math.sigmoid(β[seconds_left_])
fc = pm.Bernoulli('fc', p, observed=foul_called)
Inference¶
nba_trace = sample_from_model(nba_model)
Auto-assigning NUTS sampler... Initializing NUTS using ADVI... Average Loss = 2,955.1: 100%|██████████| 50000/50000 [00:53<00:00, 937.33it/s] Finished [100%]: Average Loss = 2,955.1 100%|██████████| 2000/2000 [02:33<00:00, 13.07it/s]
- Automatic sampler assignment (manually configurable)
- Automatic initialization of HMC/NUTS using ADVI
Model diagnostics — posterior predictions
To sample from the posterior predictive distribution, we change the value of the Theano shared variable seconds_left_.
pp_sec = np.arange(n_sec)
seconds_left_.set_value(pp_sec)
with nba_model:
pp_nba_trace = pm.sample_ppc(nba_trace, N_PP_SAMPLES)
100%|██████████| 1000/1000 [00:06<00:00, 147.16it/s]
fig
Model diagnostics — sampling
The folk theorem [of statistical computing] is this: When you have computational problems, often there’s a problem with your model.
pm.energyplot(nba_trace).legend(bbox_to_anchor=(0.6, 1));
Model selection¶
PyMC3 can calculate:
- Deviance information criterion (DIC)
- Bayesian predictive information criterion (BPIC)
- Widely applicable/Watanabe-Akaike information criterion (WAIC)
with nba_model:
nba_waic = pm.waic(nba_trace)
print(nba_waic)
WAIC_r(WAIC=5834.1378643060807, WAIC_se=79.294920797807535, p_WAIC=16.602451)
Story — take two
The trailing team has more incentive to foul than the leading team.
fig
Model and inference¶
There is a base rate at which fouls are called.
with pm.Model() as trailing_model:
α = pm.Normal('α', 0., 10.)
The trailing team is more likely to commit fouls as the game nears its end.
seconds_left_.set_value(seconds_left)
committing_trailing_ = theano.shared(1. * (score_diff < 0))
with trailing_model:
β = pm.GaussianRandomWalk('β', tau=PRIOR_PREC, init=pm.Normal.dist(0., 10.),
shape=n_sec)
η = α + committing_trailing_ * β[seconds_left_]
trailing_trace = sample_from_model(trailing_model, quiet=True)
Model diagnostics — posterior prediction
fig
Model selection¶
fig
Story — take three
Larger score differences incentivize the trailing team to foul sooner and more aggressively.
fig
Model and inference¶
There is a base rate at which fouls are called, and the trailing team is more likely to commit fouls as the game nears its end.
seconds_left_.set_value(seconds_left)
committing_trailing_ = theano.shared(1. * (score_diff < 0))
with pm.Model() as diff_model:
α = pm.Normal('α', 0., 10.)
β = pm.GaussianRandomWalk('β', tau=PRIOR_PREC, init=pm.Normal.dist(0., 10.),
shape=n_sec)
The teams trailing by more points foul more agressively and sooner.
score_diff_ = theano.shared(score_diff)
with diff_model:
γ = pm.Normal('γ', 0., 10.)
θ = pm.Normal('θ', 0., 10.)
λ = pm.math.sigmoid(γ + θ * score_diff_)
η = α + committing_trailing_ * λ * β[seconds_left_]
diff_trace = sample_from_model(diff_model, quiet=True)
fig
Model selection¶
fig
Getting started with PyMC3¶
Probabilistic Programming Ecosystem¶
| Probabilistic Programming System | Language | Discrete Variable Support | Automatic Differentiation/Hamiltonian Monte Carlo | Variational Inference |
|---|---|---|---|---|
| PyMC3 | Python | Yes | Yes | Yes |
| Stan | C++, R, Python, ... | No | Yes | Yes |
| Edward | Python, ... | Yes | Yes | Yes |
| BUGS | Standalone program, R | Yes | No | No |
| JAGS | Standalone program, R | Yes | No | No |