Open Source Bayesian Inference in Python with PyMC3¶

FOSSCON • Philadelphia • August 26, 2017¶
@AustinRochford¶
Who am I?¶

@AustinRochford • GitHub • Website¶
austin.rochford@gmail.com • arochford@monetate.com¶
PyMC3 developer • Principal Data Scientist at Monetate Labs¶
Bayesian Inference¶
A motivating question:
A rare disease is present in one out of one hundred thousand people. A test gives the correct diagnosis 99.9% of the time. What is the probability that a person that tests positive has the disease?
Conditional Probability¶
Conditional probability is the probability that one event will happen, given that another event has occured.
Our question,
A rare disease is present in one out of one hundred thousand people. A test gives the correct diagnosis 99.9% of the time. What is the probability that a person that tests positive has the disease?
becomes
0.999 * 1e-5 / (0.999 * 1e-5 + 0.001 * (1 - 1e-5))
0.009891284975940117
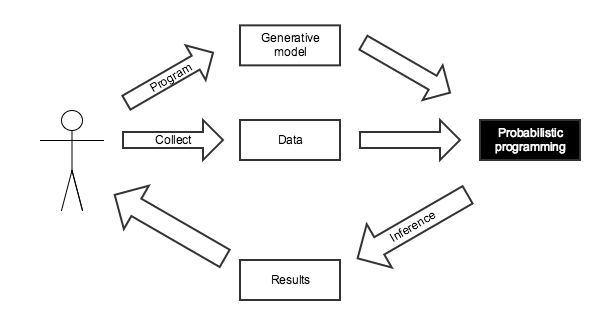
Probabilistic Programming for Bayesian Inference¶
We know the disease is present in one in one hundred thousand people.
import pymc3 as pm
with pm.Model() as disease_model:
has_disease = pm.Bernoulli('has_disease', 1e-5)
If a person has the disease, there is a 99.9% chance they test positive. If they do not have the disease, there is a 0.1% chance they test positive.
with disease_model:
p_test_pos = has_disease * 0.999 + (1 - has_disease) * 0.001
This person has tested positive for the disease.
with disease_model:
test_pos = pm.Bernoulli('test_pos', p_test_pos, observed=1)
What is the probability that this person has the disease?
with disease_model:
disease_trace = pm.sample(draws=10000, random_seed=SEED)
Assigned BinaryGibbsMetropolis to has_disease 100%|██████████| 10500/10500 [00:04<00:00, 2427.46it/s]
disease_trace['has_disease']
array([0, 0, 0, ..., 0, 0, 0])
disease_trace['has_disease'].mean()
0.0104
0.999 * 1e-5 / (0.999 * 1e-5 + 0.001 * (1 - 1e-5))
0.009891284975940117
Monte Carlo Methods¶
N = 5000
x, y = np.random.uniform(0, 1, size=(2, N))
fig
in_circle = x**2 + y**2 <= 1
fig
4 * in_circle.mean()
3.1272000000000002
History of Monte Carlo Methods¶

The Monty Hall Problem¶

Initially, we have no information about which door the prize is behind.
with pm.Model() as monty_model:
prize = pm.DiscreteUniform('prize', 0, 2)
If we choose door one:
| Prize behind | Door 1 | Door 2 | Door 3 |
|---|---|---|---|
| Door 1 | No | Yes | Yes |
| Door 2 | No | No | Yes |
| Door 2 | No | Yes | No |
from theano import tensor as tt
with monty_model:
p_open = pm.Deterministic('p_open',
tt.switch(tt.eq(prize, 0),
# it is behind the first door
np.array([0., 0.5, 0.5]),
tt.switch(tt.eq(prize, 1),
# it is behind the second door
np.array([0., 0., 1.]),
# it is behind the third door
np.array([0., 1., 0.]))))
Monty opened the third door, revealing a goat.

with monty_model:
opened = pm.Categorical('opened', p_open, observed=2)
Should we switch our choice of door?
with monty_model:
monty_trace = pm.sample(draws=10000, random_seed=SEED)
monty_df = pm.trace_to_dataframe(monty_trace)
Assigned Metropolis to prize 100%|██████████| 10500/10500 [00:02<00:00, 4427.89it/s]
monty_df.prize.head()
0 0 1 0 2 0 3 0 4 1 Name: prize, dtype: int64
fig
Yes, we should switch our choice of door.
Introduction to PyMC3¶

From the PyMC3 documentation:
PyMC3 is a Python package for Bayesian statistical modeling and Probabilistic Machine Learning which focuses on advanced Markov chain Monte Carlo and variational fitting algorithms. Its flexibility and extensibility make it applicable to a large suite of problems.

As of October 2016, PyMC3 is a NumFOCUS fiscally sponsored project.
Features¶
- Uses Theano as a computational backend
- Automated differentiation, dynamic C compilation, GPU integration
- Implements Hamiltonian Monte Carlo and No-U-Turn sampling
- High-level GLM (
R-like syntax) and Gaussian process specification - General framework for variational inference

Case Study: Sleep Deprivation¶

sleep_df.head()
| reaction | days | subject | reaction_std | |
|---|---|---|---|---|
| 0 | 249.5600 | 0 | 308 | -0.868968 |
| 1 | 258.7047 | 1 | 308 | -0.706623 |
| 2 | 250.8006 | 2 | 308 | -0.846944 |
| 3 | 321.4398 | 3 | 308 | 0.407108 |
| 4 | 356.8519 | 4 | 308 | 1.035777 |
fig
Each subject has a baseline reaction time, which should not be too far apart.
with pm.Model() as sleep_model:
μ_α = pm.Normal('μ_α', 0., 5.)
σ_α = pm.HalfCauchy('σ_α', 5.)
α = pm.Normal('α', μ_α, σ_α, shape=n_subjects)
Each subject's reaction time increases at a different rate after days of sleep deprivation.
with sleep_model:
μ_β = pm.Normal('μ_β', 0., 5.)
σ_β = pm.HalfCauchy('σ_β', 5.)
β = pm.Normal('β', μ_β, σ_β, shape=n_subjects)
The baseline reaction time and rate of increase lead to the observed reaction times.
with sleep_model:
μ = pm.Deterministic('μ', α[subject_ix] + β[subject_ix] * days)
σ = pm.HalfCauchy('σ', 5.)
obs = pm.Normal('obs', μ, σ, observed=reaction_std)
N_JOBS = 3
JOB_SEEDS = [SEED + i for i in range(N_JOBS)]
with sleep_model:
sleep_trace = pm.sample(njobs=N_JOBS, random_seed=JOB_SEEDS)
Auto-assigning NUTS sampler... Initializing NUTS using jitter+adapt_diag... 100%|██████████| 1000/1000 [00:07<00:00, 134.79it/s]
Convergence Diagnostics¶
ax = pm.energyplot(sleep_trace, legend=False)
ax.set_title("BFMI = {:.3f}".format(pm.bfmi(sleep_trace)));
max(np.max(gr_values) for gr_values in pm.gelman_rubin(sleep_trace).values())
1.0019478091296214
Prediction¶
with sleep_model:
pp_sleep_trace = pm.sample_ppc(sleep_trace)
100%|██████████| 500/500 [00:00<00:00, 1258.46it/s]
pp_df.head()
| reaction | days | subject | reaction_std | pp_0 | pp_1 | pp_10 | pp_100 | pp_101 | pp_102 | ... | pp_90 | pp_91 | pp_92 | pp_93 | pp_94 | pp_95 | pp_96 | pp_97 | pp_98 | pp_99 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 249.5600 | 0 | 308 | -0.868968 | -0.221133 | -1.094005 | -1.479840 | -0.797150 | -0.251219 | -1.846100 | ... | -0.680005 | -0.036840 | -0.618054 | 0.158745 | -0.986407 | -0.788178 | -1.483328 | -0.423254 | -0.946230 | -0.838087 |
| 1 | 258.7047 | 1 | 308 | -0.706623 | 0.354375 | -1.192640 | -0.424441 | 0.064195 | -0.661047 | -1.181403 | ... | -0.472364 | -0.825356 | -0.374235 | -0.336909 | -0.940759 | -1.236048 | -0.749208 | -0.892589 | 0.243243 | -0.891522 |
| 2 | 250.8006 | 2 | 308 | -0.846944 | 0.487935 | -0.570185 | 0.304536 | 0.758313 | 0.566803 | 0.211791 | ... | -0.512914 | 0.156596 | -0.451047 | -0.219734 | -0.773714 | -0.237561 | -0.199602 | -0.071147 | 0.146439 | -0.193735 |
| 3 | 321.4398 | 3 | 308 | 0.407108 | 0.950116 | -0.554748 | 0.544648 | 1.037173 | -0.245327 | 0.450455 | ... | -0.183340 | 0.289252 | 0.358078 | 1.579609 | 0.652802 | -0.286667 | -0.327654 | 0.607906 | -0.087981 | -0.097427 |
| 4 | 356.8519 | 4 | 308 | 1.035777 | 0.485269 | 0.549079 | 0.564043 | 0.045464 | 0.643697 | 0.190714 | ... | 0.976137 | 0.306833 | 0.744076 | 0.493216 | 0.516644 | 1.090693 | 0.583320 | 1.079374 | 0.996899 | 0.671175 |
5 rows × 504 columns
grid.fig
Hamiltonian Monte Carlo in PyMC3¶
mcmc_fig
The Curse of Dimensionality¶
fig
Hamiltonian Monte Carlo¶

x = tt.dscalar('x')
x.tag.test_value = 0.
y = x**3
from theano import pprint
pprint(tt.grad(y, x))
'((fill((x ** TensorConstant{3}), TensorConstant{1.0}) * TensorConstant{3}) * (x ** (TensorConstant{3} - TensorConstant{1})))'
Case Study: 1984 Congressional Votes¶
vote_df.head()
| rep_id | party | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | republican | n | y | n | y | y | y | n | n | n | y | ? | y | y | y | n | y |
| 1 | 1 | republican | n | y | n | y | y | y | n | n | n | n | n | y | y | y | n | ? |
| 2 | 2 | democrat | ? | y | y | ? | y | y | n | n | n | n | y | n | y | y | n | n |
| 3 | 3 | democrat | n | y | y | n | ? | y | n | n | n | n | y | n | y | n | n | y |
| 4 | 4 | democrat | y | y | y | n | y | y | n | n | n | n | y | ? | y | y | y | y |
Question: can we separate Democrats and Republicans based on their voting records?
grid.fig
Latent State Model
- Representatives ($\color{blue}{\theta_i}$) and bills ($\color{green}{b_j})$ have ideal points on a liberal-conservative spectrum.
- If the ideal points are equal, there is a 50% chance the representative will vote for the bill.
with pm.Model() as vote_model:
# representative ideal points
θ = pm.Normal('θ', 0., 1., shape=n_rep)
# bill ideal points
a = hierarchical_normal('a', N_BILL)
- Bills also have an ability to discriminate ($\color{red}{a_j}$) between conservative and liberal representatives.
- Some bills have broad bipartisan support, while some provoke votes along party lines.
with vote_model:
# bill discrimination parameters
b = hierarchical_normal('b', N_BILL)
This model has
n_rep + 2 * (N_BILL + 1)
469
parameters
Observation Model
$$ \begin{align*} P(\textrm{Representative }i \textrm{ votes for bill }j\ |\ \color{blue}{\theta_i}, \color{green}{b_j}, \color{red}{a_j}) & = \frac{1}{1 + \exp\left(-\left(\color{red}{a_j} \cdot \color{blue}{\theta_i} - \color{green}{b_j}\right)\right)} \end{align*} $$fig
with vote_model:
η = a[bill_id] * θ[rep_id] - b[bill_id]
p = pm.math.sigmoid(η)
obs = pm.Bernoulli('obs', p, observed=vote)
Hamiltonian Monte Carlo Inference
with vote_model:
nuts_trace = pm.sample(init='adapt_diag', njobs=N_JOBS,
random_seed=JOB_SEEDS)
Auto-assigning NUTS sampler... Initializing NUTS using adapt_diag... 100%|██████████| 1000/1000 [02:11<00:00, 12.76it/s]
Convergence Diagnostics¶
ax = pm.energyplot(nuts_trace, legend=False)
ax.set_title("BFMI = {:.3f}".format(pm.bfmi(nuts_trace)));
max(np.max(gr_values) for gr_values in pm.gelman_rubin(nuts_trace).values())
1.0135857288309107
Ideal Points¶
fig
Discriminative Ability of Bills¶
pm.forestplot(nuts_trace, varnames=['a'], rhat=False, xtitle="$a$",
ylabels=["Bill {}".format(i + 1) for i in range(N_BILL)]);
Comparison to Non-Hamiltonian MCMC¶
with vote_model:
step = pm.Metropolis()
met_trace_ = pm.sample(10000, step, njobs=N_JOBS, random_seed=JOB_SEEDS)
met_trace = met_trace_[5000::5]
100%|██████████| 10500/10500 [03:40<00:00, 47.65it/s]
max(np.max(gr_values) for gr_values in pm.gelman_rubin(met_trace).values())
39.87901257961822
fig
Next Steps¶
PyMC3¶
|
|

|

|
Probabilistic Programming Ecosystem¶
| Probabilistic Programming System | Language | License | Discrete Variable Support | Automatic Differentiation/Hamiltonian Monte Carlo | Variational Inference |
|---|---|---|---|---|---|
| PyMC3 | Python | Apache V2 | Yes | Yes | Yes |
| Stan | C++, R, Python, ... | BSD 3-clause | No | Yes | Yes |
| Edward | Python, ... | Apache V2 | Yes | Yes | Yes |
| BUGS | Standalone program, R | GPL V2 | Yes | No | No |
| JAGS | Standalone program, R | GPL V2 | Yes | No | No |
Thank you!¶

@AustinRochford • austin.rochford@gmail.com • arochford@monetate.com¶
The Jupyter notebook used to generate these slides is available here.