The Importance of Sequential Testing

As the world becomes ever more data-driven, the basic theory of hypothesis testing is being used by more people and in more contexts than ever before. This epansion has, however, come with a cost. The dominant Neyman-Pearson hypothesis testing framework is subtle and easy to unknowingly misuse. In this post, we’ll explore the common scenario where we would like to monitor the status of an ongoing experiment and stop the experiment early if an effect becomes apparent.

There are many situations in which it is advantageous to monitor the status of an experiment and terminate it early if the conclusion seems apparent. In business, experiments cost money, both in terms of the actual cost of data collection and in terms of the opportunity cost of waiting for an experiment to reach a set number of samples before acting on its outcome, which may have been apparent much earlier. In medicine, it may be unethical to continue an experimental treatment which appears to have a detrimental effect, or to deny the obviously better experimental treatment to the control group until the predetermined sample size is reached.

While these reasons for continuous monitoring and early termination of certain experiments are quite compelling, if this method is applied naively, it can lead to wildly incorrect analyses. Below, we illustrate the perils of the naive approach to sequential testing (as this sort of procedure is known) and show how to perform a correct analysis of a fairly simple, yet illustrative introductory sequential experiment.

A brief historical digression may be informative. The frequentist approach to hypothesis testing was pioneered just after the turn of the 20th century in England in order to analyze agricultural experiments. According to Armitage, one of the pioneers of sequential experiment design:

[t]he classical theory of experimental design deals predominantly with experiments of predetermined size, presumably because the pioneers of the subject, particularly R. A. Fisher, worked in agricultural research, where the outcome of a field trial is not available until long after the experiment has been designed and started. It is interesting to speculate how differently statistical theory might have evolved if Fisher had been employed in medical or industrial research.¹

In this post, we will analyze the following hypothesis test. Assume the data are drawn from the normal distribution, \(N(\theta, 1)\) with unknown mean \(\theta\) and known variance \(\sigma^2 = 1\). We wish to test the simple null hypothesis that \(\theta = 0\) versus the simple alternative hypothesis that \(\theta = 1\) at the \(\alpha = 0.05\) level. By the Neyman-Pearson lemma, the most powerful test of this hypothesis rejects the null hypothesis when the likelihood ratio exceeds some critical value. In our normal case, it is well-known that this criterion is equivalent to \(\sum_{i = 1}^n X_i > \sqrt{n} z_{0.05}\) where \(z_{0.05} \approx 1.64\) is the \(1 - 0.05 = 0.95\) quantile of the standard normal distribution.

To model the ongoing monitoring of this experiment, we define a random variable \(N = \min \{n \geq 1 | \sum_{i = 1}^n X_i > \sqrt{n} z_{0.05}\}\), called the stopping time. The random variable \(N\) is the first time that the test statistic exceeds the critical value, and the naive approach to sequential testing would reject the null hypothesis after \(N\) samples (when \(N < \infty\), of course). At first, this procedure may seem reasonable, because when the alternative hypothesis that \(\theta = 1\) is true, \(N < \infty\) almost surely by the strong law of large numbers. The first inkling that something is amiss with this procedure is the surprising fact that it is also true that \(N < \infty\) almost surely under the null hypothesis that \(\theta = 0\). (See Keener² for a proof.) More informally, if we sample long enough, this procedure will almost always reject the null hypothesis, even when it is true.

To illustrate this problem more quantitatively, consider the following simulation. Suppose we decide ahead of time that we will stop the experiment when the critical value for the current sample size is exceeded, in which case we reject the null hypothesis, or we have collected one thousand samples without exceeding the critical value at any point, in which case we accept the null hypothesis.

Here we use a Monte Carlo method to approximate the level of this naive sequential test. First we generate ten thousand simulations of such an experiment, assuming the null hypothesis that the data are \(N(0, 1)\) is true.

from __future__ import division

import numpy as np
from scipy import stats

n = 100
N = 10000

samples = stats.norm.rvs(size=(N, n))

Here each row of samples corresponds to a simulation and each column to a sample.

Now we calculate the proportion of these simulated experiments that would have been stopped before one thousand samples, incorrectly rejecting the null hypothesis.

alpha = 0.05
z_alpha = stats.norm.isf(alpha)

cumsums = samples.cumsum(axis=1)
ns = np.arange(1, n + 1)

np.any(cumsums > np.sqrt(ns) * z_alpha, axis=1).sum() / N

0.30909999999999999

Here, each row of cumsums corresponds to a simulation and each column to the value of the test statistic \(\sum_{i = 1}^k X_i\) after \(k\) observations.

We see that the actual level of this test is an order of magnitude larger than the desired level of \(\alpha = 0.05\). To check that our method is reasonable, we see that if we always collect one thousand samples, we achieve a simulated level quite close to \(\alpha = 0.05\).

(cumsums[:, -1] > np.sqrt(n) * z_alpha).sum() / N

0.051700000000000003

This simulation is compelling evidence that the naive approach to sequential testing is not correct.

Fortunately, the basic framework for the correct analysis of sequential experiments was worked out during World War II to more efficiently test lots of ammunition (among other applications). In 1947, Wald introduced the sequential probability ratio test (SPRT), which produces a correct analysis of the experiment we have been considering.

Let

\[ \begin{align*} \Lambda (x_1, \ldots, x_n) & = \frac{L(1; x_1, \ldots, x_n)}{L(0; x_1, \ldots, x_n)} \end{align*} \]

be the likelihood ratio corresponding to our two hypotheses. The SPRT uses two thresholds, \(0 < a < 1 < b\), and continues sampling whenever \(a < \Lambda (x_1, \ldots, x_n) < b\). When \(\Lambda (x_1, \ldots, x_n) \leq a\), we accept the null hypothesis, and when \(b \leq \Lambda (x_1, \ldots, x_n)\), we reject the null hypothesis. We choose \(A\) and \(B\) by fixing the approximate level of the test, \(\alpha\), and the approximate power of the test, \(1 - \beta\). With these quantities chosen, we use

\[ \begin{align*} a & = \frac{\beta}{1 - \alpha}, \textrm{and} \\ b & = \frac{1 - \beta}{\alpha}. \end{align*} \]

For our hypothesis test \(\alpha = 0.05\). The power of the naive test after \(n\) samples is

power = 1 - stats.norm.sf(z_alpha - 1 / np.sqrt(n))
beta = 1 - power

power

0.93880916378665569

Which gives the following values for \(a\) and \(b\):

a = beta / (1 - alpha)
b = (1 - beta) / alpha

a, b

(0.06441140654036244, 18.776183275733114)

For our example, it will be benificial to rewrite the SPRT in terms of the log- likelihood ratio,

\[ \begin{align*} \log a & < \log \Lambda (x_1, \ldots, x_n) < \log b. \end{align*} \]

It is easy to show that \(\log \Lambda (x_1, \ldots, x_n) = \frac{n}{2} - \sum_{i = 1}^n X_i\), so the SPRT in this case reduces to

\[ \begin{align*} \frac{n}{2} - \log b & < \sum_{i = 1}^n X_i < \frac{n}{2} - \log a. \end{align*} \]

The logarithms of \(a\) and \(b\) are

np.log((a, b))

array([-2.74246454,  2.93258922])

We verify that this test is indeed of approximate level \(\alpha = 0.05\) using the simulations from our previous Monte Carlo analysis.

np.any(cumsums >= ns / 2 - np.log(a), axis=1).sum() / N

0.036299999999999999

The following plot shows the rejection boundaries for both the naive sequential test and the SPRT along with the density of our Monte Carlo samples.

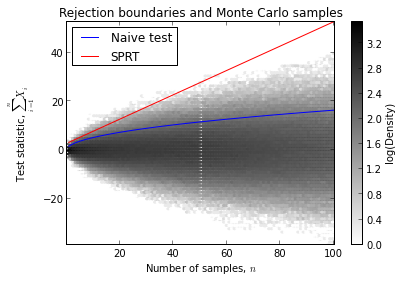
From this diagram we can easily see that a significant number of samples fall above the rejection boundary for the naive test (the blue curve) but below the rejection boundary for the SPRT (the red line). These samples explain the large discrepancy between the desired level of the test (\(\alpha = 0.05\)) and the simulated level of the naive test. We also see that very few samples exceed the rejection boundary for the SPRT, leading it to have level smaller than \(\alpha = 0.05\).

It is important to note that we have barely scratched the surface of the vast field of sequential experiment design and analysis. We have not even attempted to give more than a cursory introduction to the SPRT, one of the most basic ideas in this field. One property of this test that bears mentioning is its optimality, in the following sense. Just as the Neyman-Pearson lemma shows that the likelihood ratio test is the most powerful test of a simple hypothesis at a fixed level, the Wald-Wolfowitz theorem shows that the SPRT is the sequential test that minimizes the expected stopping time under both the null and alternative hypotheses for a fixed level and power. For more details on this theorem, and the general theory of sequential experiments, consult Bartroff et al.³.

This post is available as an IPython notebook here.

Discussion on Hacker News