An Improved Analysis of NBA Foul Calls with Python
Last April, I wrote a post that used Bayesian item-response theory models to analyze NBA foul call data. Last November, I spoke about a greatly improved version of these models at PyData NYC. This post is a write-up of the models from that talk.
Last Two-minute Report
Since late in the 2014-2015 season, the NBA has issued last two minute reports. These reports give the league’s assessment of the correctness of foul calls and non-calls in the last two minutes of any game where the score difference was three or fewer points at any point in the last two minutes.
These reports are notably different from play-by-play logs, in that they include information on non-calls for notable on-court interactions. This non-call information presents a unique opportunity to study the factors that impact foul calls. There is a level of subjectivity inherent in the the NBA’s definition of notable on-court interactions which we attempt to mitigate later using season-specific factors.
Loading the data
Russel Goldenberg of The Pudding has been scraping the PDFs that the NBA publishes and transforming them into a CSV for some time. I am grateful for his work, which has enabled this analysis.
We download the data locally to be kind to GitHub.
%matplotlib inlineimport datetime
from itertools import product
import logging
import picklefrom matplotlib import pyplot as plt
from matplotlib.offsetbox import AnchoredText
from matplotlib.ticker import FuncFormatter, StrMethodFormatter
import numpy as np
import pandas as pd
import scipy as sp
import seaborn as sns
from sklearn.preprocessing import LabelEncoder
from theano import tensor as ttpct_formatter = StrMethodFormatter('{x:.1%}')
sns.set()
blue, green, *_ = sns.color_palette()
plt.rc('figure', figsize=(8, 6))
LABELSIZE = 14
plt.rc('axes', labelsize=LABELSIZE)
plt.rc('axes', titlesize=LABELSIZE)
plt.rc('figure', titlesize=LABELSIZE)
plt.rc('legend', fontsize=LABELSIZE)
plt.rc('xtick', labelsize=LABELSIZE)
plt.rc('ytick', labelsize=LABELSIZE)SEED = 207183 # from random.org, for reproducibility# keep theano from complaining about compile locks for small models
(logging.getLogger('theano.gof.compilelock')
.setLevel(logging.CRITICAL))%%bash
DATA_URI=https://raw.githubusercontent.com/polygraph-cool/last-two-minute-report/32f1c43dfa06c2e7652cc51ea65758007f2a1a01/output/all_games.csv
DATA_DEST=/tmp/all_games.csv
if [[ ! -e $DATA_DEST ]];
then
wget -q -O $DATA_DEST $DATA_URI
fiWe use only a subset of the columns in the source data set.
USECOLS = [
'period',
'seconds_left',
'call_type',
'committing_player',
'disadvantaged_player',
'review_decision',
'play_id',
'away',
'home',
'date',
'score_away',
'score_home',
'disadvantaged_team',
'committing_team'
]orig_df = pd.read_csv(
'/tmp/all_games.csv',
usecols=USECOLS,
index_col='play_id',
parse_dates=['date']
)The data set contains more than 16,000 plays.
orig_df.shape[0]16300Each row of the DataFrame represents a play and each column describes an attrbiute of the play:
-
periodis the period of the game, -
seconds_leftis the number of seconds remaining in the game, -
call_typeis the type of call, -
committing_playeranddisadvantaged_playerare the names of the players involved in the play, -
review_decisionis the opinion of the league reviewer on whether or not the play was called correctly:-
review_decision = "INC"means the call was an incorrect noncall, -
review_decision = "CNC"means the call was an correct noncall, -
review_decision = "IC"means the call was an incorrect call, and -
review_decision = "CC"means the call was an correct call,
-
-
awayandhomeare the abbreviations of the teams involved in the game, -
dateis the date on which the game was played, -
score_awayandscore_homeare the scores of theawayandhometeam during the play, respectively, and -
disadvantaged_teamandcommitting_teamindicate how each team is involved in the play.
orig_df.head(n=2).T| play_id | 20150301CLEHOU-0 | 20150301CLEHOU-1 |
|---|---|---|
| period | Q4 | Q4 |
| seconds_left | 112 | 103 |
| call_type | Foul: Shooting | Foul: Shooting |
| committing_player | Josh Smith | J.R. Smith |
| disadvantaged_player | Kevin Love | James Harden |
| review_decision | CNC | CC |
| away | CLE | CLE |
| home | HOU | HOU |
| date | 2015-03-01 00:00:00 | 2015-03-01 00:00:00 |
| score_away | 103 | 103 |
| score_home | 105 | 105 |
| disadvantaged_team | CLE | HOU |
| committing_team | HOU | CLE |
Research questions
In this post, we answer two questions:
- How does game context impact foul calls?
- Is (not) committing and/or drawing fouls a measurable player skill?
The previous post focused on the second question, and gave the first question only a cursory treatment. This post enhances our treatment of the first question, in order to control for non-skill factors influencing foul calls (namely intentional fouls). Controlling for these factors makes our estimates of player skill more realistic.
Exploratory Data Analysis
First we examine the types of calls present in the data set.
(orig_df['call_type']
.value_counts()
.head(n=15))Foul: Personal 4736
Foul: Shooting 4201
Foul: Offensive 2846
Foul: Loose Ball 1316
Turnover: Traveling 779
Instant Replay: Support Ruling 607
Foul: Defense 3 Second 277
Instant Replay: Overturn Ruling 191
Foul: Personal Take 172
Turnover: 3 Second Violation 139
Turnover: 24 Second Violation 126
Turnover: 5 Second Inbound 99
Stoppage: Out-of-Bounds 96
Violation: Lane 84
Foul: Away from Play 82
Name: call_type, dtype: int64The portion of call_type before the colon is the general category of the call. We count the occurence of these categories below.
(orig_df['call_type']
.str.split(':', expand=True)
.iloc[:, 0]
.value_counts()
.plot(
kind='bar',
color=blue, logy=True,
title="Call types"
)
.set_ylabel("Frequency"));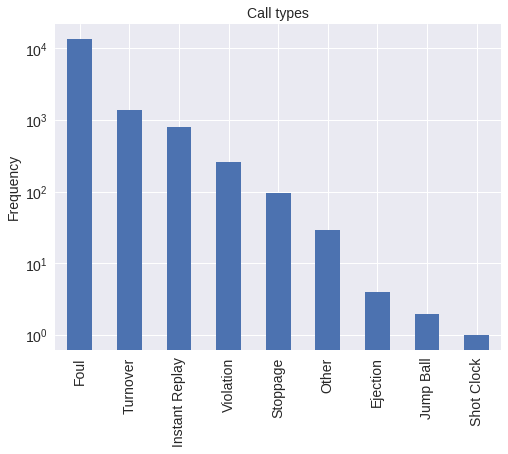
We restrict our attention to foul calls, though other call types would be interesting to study in the future.
foul_df = orig_df[
orig_df['call_type']
.fillna("UNKNOWN")
.str.startswith("Foul")
]We count the foul call types below.
(foul_df['call_type']
.str.split(': ', expand=True)
.iloc[:, 1]
.value_counts()
.plot(
kind='bar',
color=blue, logy=True,
title="Foul Types"
)
.set_ylabel("Frequency"));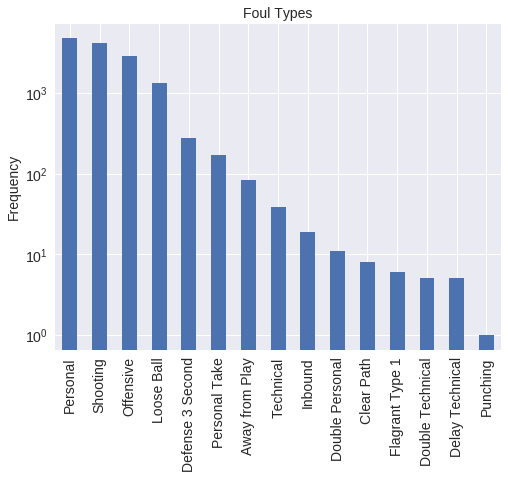
We restrict our attention to the five foul types below, which generally involve two players. This subset of fouls allows us to pursue our second research question in the most direct manner.
FOULS = [
f"Foul: {foul_type}"
for foul_type in [
"Personal",
"Shooting",
"Offensive",
"Loose Ball",
"Away from Play"
]
]Data transformation
There are a number of misspelled team names in the data, which we correct.
TEAM_MAP = {
"NKY": "NYK",
"COS": "BOS",
"SAT": "SAS",
"CHi": "CHI",
"LA)": "LAC",
"AT)": "ATL",
"ARL": "ATL"
}
def correct_team_name(col):
def _correct_team_name(df):
return df[col].apply(lambda team_name: TEAM_MAP.get(team_name, team_name))
return _correct_team_nameWe also convert each game date to an NBA season.
def date_to_season(date):
if date >= datetime.datetime(2017, 10, 17):
return '2017-2018'
elif date >= datetime.datetime(2016, 10, 25):
return '2016-2017'
elif date >= datetime.datetime(2015, 10, 27):
return '2015-2016'
else:
return '2014-2015'We clean the data by
- restricting to plays that occured during the last two minutes of regulation,
- imputing incorrect noncalls when
review_decisionis missing, - correcting team names,
- converting game dates to seasons,
- restricting to the foul types discussed above,
- restricting to the plays that happened during the 2015-2016 and 2016-2017 regular seasons (those are the only full seasons in the data set as of February 2018), and
- dropping unneeded rows and columns.
clean_df = (foul_df.where(lambda df: df['period'] == "Q4")
.where(lambda df: (df['date'].between(datetime.datetime(2016, 10, 25),
datetime.datetime(2017, 4, 12))
| df['date'].between(datetime.datetime(2015, 10, 27),
datetime.datetime(2016, 5, 30)))
)
.assign(
review_decision=lambda df: df['review_decision'].fillna("INC"),
committing_team=correct_team_name('committing_team'),
disadvantged_team=correct_team_name('disadvantaged_team'),
away=correct_team_name('away'),
home=correct_team_name('home'),
season=lambda df: df['date'].apply(date_to_season)
)
.where(lambda df: df['call_type'].isin(FOULS))
.dropna()
.drop('period', axis=1)
.assign(call_type=lambda df: (df['call_type']
.str.split(': ', expand=True)
.iloc[:, 1])))About 55% of the rows in the original data set remain.
clean_df.shape[0] / orig_df.shape[0]0.5516564417177914clean_df.head(n=2).T| play_id | 20151028INDTOR-1 | 20151028INDTOR-2 |
|---|---|---|
| seconds_left | 89 | 73 |
| call_type | Shooting | Shooting |
| committing_player | Ian Mahinmi | Bismack Biyombo |
| disadvantaged_player | DeMar DeRozan | Paul George |
| review_decision | CC | IC |
| away | IND | IND |
| home | TOR | TOR |
| date | 2015-10-28 00:00:00 | 2015-10-28 00:00:00 |
| score_away | 99 | 99 |
| score_home | 106 | 106 |
| disadvantaged_team | TOR | IND |
| committing_team | IND | TOR |
| disadvantged_team | TOR | IND |
| season | 2015-2016 | 2015-2016 |
We use scikit-learn’s LabelEncoder to transform categorical features (call type, player, and season) to integers.
call_type_enc = LabelEncoder().fit(
clean_df['call_type']
)
n_call_type = call_type_enc.classes_.size
player_enc = LabelEncoder().fit(
np.concatenate((
clean_df['committing_player'],
clean_df['disadvantaged_player']
))
)
n_player = player_enc.classes_.size
season_enc = LabelEncoder().fit(
clean_df['season']
)
n_season = season_enc.classes_.sizeWe transform the data by
- rounding
seconds_leftto the nearest second (purely for convenience), - transforming categorical features to integer ids,
- setting
foul_calledequal to one or zero depending on whether or not a foul was called, and - setting
score_committingandscore_disadvantagedto the score of the committing and disadvantaged teams, respectively.
df = (clean_df[['seconds_left']]
.round(0)
.assign(
call_type=call_type_enc.transform(clean_df['call_type']),
foul_called=1. * clean_df['review_decision'].isin(['CC', 'INC']),
player_committing=player_enc.transform(clean_df['committing_player']),
player_disadvantaged=player_enc.transform(clean_df['disadvantaged_player']),
score_committing=clean_df['score_home'].where(
clean_df['committing_team'] == clean_df['home'],
clean_df['score_away']
),
score_disadvantaged=clean_df['score_home'].where(
clean_df['disadvantaged_team'] == clean_df['home'],
clean_df['score_away']
),
season=season_enc.transform(clean_df['season'])
))The resulting data is ready for analysis.
df.head(n=2).T| play_id | 20151028INDTOR-1 | 20151028INDTOR-2 |
|---|---|---|
| seconds_left | 89.0 | 73.0 |
| call_type | 4.0 | 4.0 |
| foul_called | 1.0 | 0.0 |
| player_committing | 162.0 | 36.0 |
| player_disadvantaged | 98.0 | 358.0 |
| score_committing | 99.0 | 106.0 |
| score_disadvantaged | 106.0 | 99.0 |
| season | 0.0 | 0.0 |
Modeling
We follow George Box’s modeling workflow, as summarized by Dustin Tran:
- build a model of the science,
- infer the model given data, and
- criticize the model given data.
Baseline model
Build a model of the science
Below we examine the foul call rate by season.
def make_foul_rate_yaxis(ax, label="Observed foul call rate"):
ax.yaxis.set_major_formatter(pct_formatter)
ax.set_ylabel(label)
return ax
make_foul_rate_yaxis(
df.pivot_table('foul_called', 'season')
.rename(index=season_enc.inverse_transform)
.rename_axis("Season")
.plot(kind='bar', rot=0, legend=False)
);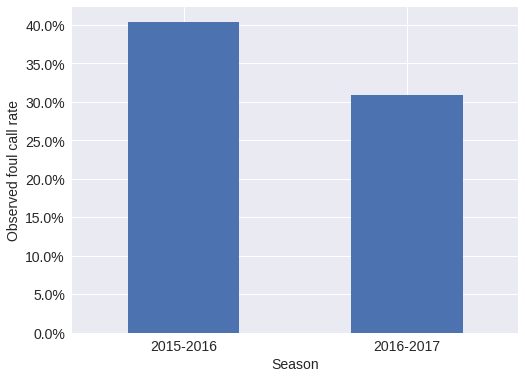
There is a pronounced difference between the foul call rate in the 2015-2016 and 2016-2017 NBA seasons; our first model accounts for this difference.
We use pymc3 to specify our models. Our first model is given by
\[ \begin{align*} \beta^{\textrm{season}}_s & \sim N(0, 5) \\ \eta^{\textrm{game}}_k & = \beta^{\textrm{season}}_{s(k)} \\ p_k & = \textrm{sigm}\left(\eta^{\textrm{game}}_k\right). \end{align*} \]
We use a logistic regression model with different factors for each season.
import pymc3 as pm
with pm.Model() as base_model:
β_season = pm.Normal('β_season', 0., 5., shape=n_season)
p = pm.Deterministic('p', pm.math.sigmoid(β_season))Foul calls are Bernoulli trials, \(y_k \sim \textrm{Bernoulli}(p_k).\)
season = df['season'].valueswith base_model:
y = pm.Bernoulli(
'y', p[season],
observed=df['foul_called']
)Infer the model given data
We now sample from the model’s posterior distribution.
NJOBS = 3
SAMPLE_KWARGS = {
'draws': 1000,
'njobs': NJOBS,
'random_seed': [
SEED + i for i in range(NJOBS)
],
'nuts_kwargs': {
'target_accept': 0.9
}
}with base_model:
base_trace = pm.sample(**SAMPLE_KWARGS)Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (3 chains in 3 jobs)
NUTS: [β_season]
100%|██████████| 1500/1500 [00:07<00:00, 198.65it/s]Convergence diagnostics
We rely on three diagnostics to ensure that our samples have converged to the posterior distribution:
- Energy plots: if the two distributions in the energy plot differ significantly (espescially in the tails), the sampling was not very efficient.
- Bayesian fraction of missing information (BFMI): BFMI quantifies this difference with a number between zero and one. A BFMI close to (or exceeding) one is preferable, and a BFMI lower than 0.2 is indicative of efficiency issues.
- Gelman-Rubin statistics: Gelman-Rubin statistics near one are preferable, and values less than 1.1 are generally taken to indicate convergence.
For more information on energy plots and BFMI consult Robust Statistical Workflow with PyStan.
bfmi = pm.bfmi(base_trace)
max_gr = max(
np.max(gr_stats) for gr_stats in pm.gelman_rubin(base_trace).values()
)CONVERGENCE_TITLE = lambda: f"BFMI = {bfmi:.2f}\nGelman-Rubin = {max_gr:.3f}"(pm.energyplot(base_trace, legend=False, figsize=(6, 4))
.set_title(CONVERGENCE_TITLE()));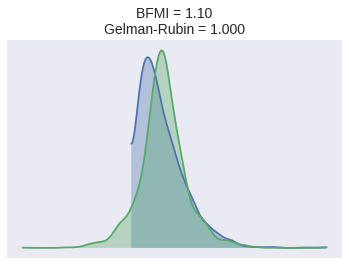
Criticize the model given data
We use the samples from p’s posterior distribution to calculate residuals, which we use to criticize our models. These residuals allow us to assess how well our model describes the data-generation process and to discover unmodeled sources of variation.
base_trace['p']array([[ 0.4052151 , 0.30696232],
[ 0.3937377 , 0.30995026],
[ 0.39881138, 0.29866616],
...,
[ 0.40279887, 0.31166828],
[ 0.4077945 , 0.30299785],
[ 0.40207901, 0.29991789]])resid_df = (df.assign(p_hat=base_trace['p'][:, df['season']].mean(axis=0))
.assign(resid=lambda df: df['foul_called'] - df['p_hat']))resid_df[['foul_called', 'p_hat', 'resid']].head()| foul_called | p_hat | resid | |
|---|---|---|---|
| play_id | |||
| 20151028INDTOR-1 | 1.0 | 0.403875 | 0.596125 |
| 20151028INDTOR-2 | 0.0 | 0.403875 | -0.403875 |
| 20151028INDTOR-3 | 1.0 | 0.403875 | 0.596125 |
| 20151028INDTOR-4 | 0.0 | 0.403875 | -0.403875 |
| 20151028INDTOR-6 | 0.0 | 0.403875 | -0.403875 |
The per-season residuals are quite small, which is to be expected.
(resid_df.pivot_table('resid', 'season')
.rename(index=season_enc.inverse_transform))| resid | |
|---|---|
| season | |
| 2015-2016 | -0.000162 |
| 2016-2017 | -0.000219 |
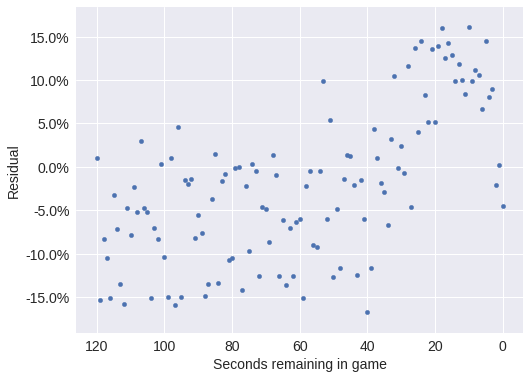
Anyone who has watched a close basketball game will realize that we have neglected an important factor in late game foul calls — intentional fouls. Near the end of the game, intentional fouls are used by the losing team when they are on defense to end the leading team’s possession as quickly as possible.
The influence of intentional fouls in the plot below is shown by the rapidly increasing of the residuals as the number of seconds left in the game decreases.
def make_time_axes(ax,
xlabel="Seconds remaining in game",
ylabel="Observed foul call rate"):
ax.invert_xaxis()
ax.set_xlabel(xlabel)
return make_foul_rate_yaxis(ax, label=ylabel)
make_time_axes(
resid_df.pivot_table('resid', 'seconds_left')
.reset_index()
.plot('seconds_left', 'resid', kind='scatter'),
ylabel="Residual"
);
Possession model
Build a model of the science
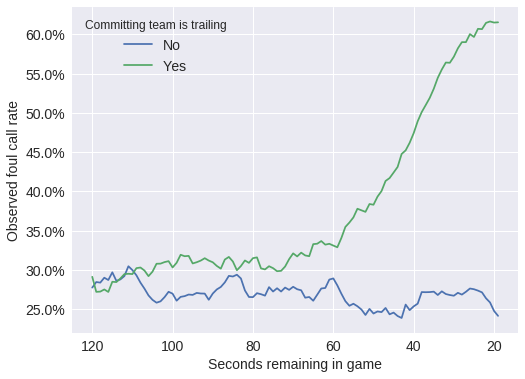
The following plot illustrates the fact that only the trailing team has any incentive to committ intentional fouls.
df['trailing_committing'] = (df['score_committing']
.lt(df['score_disadvantaged'])
.mul(1.)
.astype(np.int64))make_time_axes(
df.pivot_table(
'foul_called',
'seconds_left',
'trailing_committing'
)
.rolling(20)
.mean()
.rename(columns={
0: "No", 1: "Yes"
})
.rename_axis(
"Committing team is trailing",
axis=1
)
.plot()
);
Intentional fouls are only useful when the trailing (and committing) team is on defense. The plot below reflects this fact; shooting and personal fouls are almost always called against the defensive player; we see that they are called at a much higher rate than offensive fouls.
ax = (df.pivot_table('foul_called', 'call_type')
.rename(index=call_type_enc.inverse_transform)
.rename_axis("Call type", axis=0)
.plot(kind='barh', legend=False))
ax.xaxis.set_major_formatter(pct_formatter);
ax.set_xlabel("Observed foul call rate");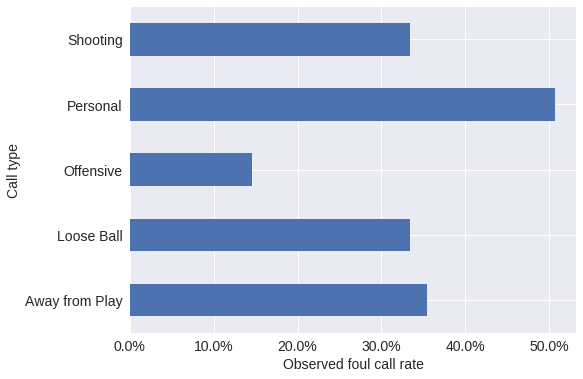
We continue to model the differnce in foul call rates between seasons.
with pm.Model() as poss_model:
β_season = pm.Normal('β_season', 0., 5., shape=2)Throughout this post, we will use hierarchical distributions to model the variation of foul call rates. For much more information on hierarchical models, consult Data Analysis Using Regression and Multilevel/Hierarchical Models. We use the priors
\[ \begin{align*} \sigma_{\textrm{call}} & \sim \operatorname{HalfNormal}(5) \\ \beta^{\textrm{call}}_{c} & \sim \operatorname{Hierarchical-Normal}(0, \sigma_{\textrm{call}}^2). \end{align*} \]
For sampling efficiency, we use an [non-centered parametrization](http://twiecki.github.io/blog/2017/02/08/bayesian-hierchical-non-centered/#The-Funnel-of-Hell-(and-how-to-escape-it%29) of the hierarchical normal distribution.
def hierarchical_normal(name, shape, σ_shape=1):
Δ = pm.Normal(f'Δ_{name}', 0., 1., shape=shape)
σ = pm.HalfNormal(f'σ_{name}', 5., shape=σ_shape)
return pm.Deterministic(name, Δ * σ)Each call type has a different foul call rate.
with poss_model:
β_call = hierarchical_normal('β_call', n_call_type)We add score difference and the number of possessions by which the committing team is trailing to the DataFrame.
df['score_diff'] = (df['score_disadvantaged']
.sub(df['score_committing']))
df['trailing_poss'] = (df['score_diff']
.div(3)
.apply(np.ceil))trailing_poss_enc = LabelEncoder().fit(df['trailing_poss'])
trailing_poss = trailing_poss_enc.transform(df['trailing_poss'])
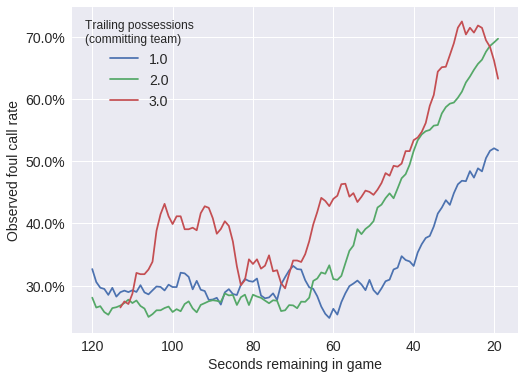
n_trailing_poss = trailing_poss_enc.classes_.sizeThe plot below shows that the foul call rate (over time) varies based on the score difference (quantized into possessions) between the disadvanted team and the committing team. We assume that at most three points can be scored in a single possession (while this is not quite correct, four-point plays are rare enough that we do not account for them in our analysis).
make_time_axes(
df.pivot_table(
'foul_called',
'seconds_left',
'trailing_poss'
)
.loc[:, 1:3]
.rolling(20).mean()
.rename_axis(
"Trailing possessions\n(committing team)",
axis=1
)
.plot()
);
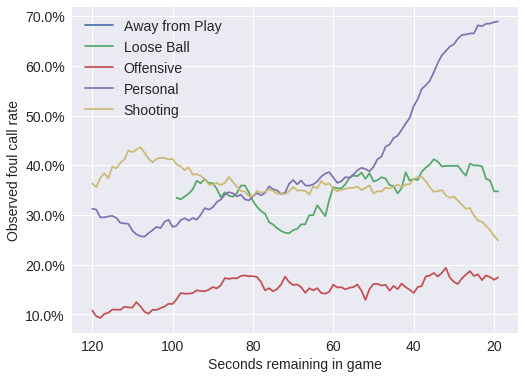
The plot below reflects the fact that intentional fouls are disproportionately personal fouls; the rate at which personal fouls are called increases drastically as the game nears its end.
make_time_axes(
df.pivot_table('foul_called', 'seconds_left', 'call_type')
.rolling(20).mean()
.rename(columns=call_type_enc.inverse_transform)
.rename_axis(None, axis=1)
.plot()
);
Due to the NBA’s shot clock, the natural timescale of a basketball game is possessions, not seconds, remaining.
df['remaining_poss'] = (df['seconds_left']
.floordiv(25)
.add(1))remaining_poss_enc = LabelEncoder().fit(df['remaining_poss'])
remaining_poss = remaining_poss_enc.transform(df['remaining_poss'])
n_remaining_poss = remaining_poss_enc.classes_.sizeBelow we plot the foul call rate across trailing possession/remaining posession pairs. Note that we always calculate trailing possessions (trailing_poss) from the perspective of the committing team. For instance, trailing_poss = 1 indicates that the committing team is trailing by 1-3 points, whereas trailing_poss = -1 indicates that the committing team is leading by 1-3 points.
ax = sns.heatmap(
df.pivot_table(
'foul_called',
'trailing_poss',
'remaining_poss'
)
.rename_axis(
"Trailing possessions\n(committing team)",
axis=0
)
.rename_axis("Remaining possessions", axis=1),
cmap='seismic',
cbar_kws={'format': pct_formatter}
)
ax.invert_yaxis();
ax.set_title("Observed foul call rate");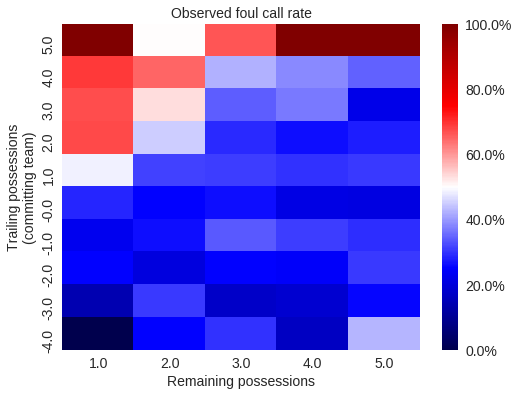
The heatmap above shows that the foul call rate increases significantly when the committing team is trailing by more than the number of possessions remaining in the game. That is, teams resort to intentional fouls only when the opposing team can run out the clock and guarantee a win. (Since we have quantized the score difference and time into posessions, this conclusion is not entirely correct; it is, however, correct enough for our purposes.)
call_name_df = df.assign(
call_type=lambda df: call_type_enc.inverse_transform(
df['call_type'].values
)
)
diff_df = (pd.merge(
call_name_df,
call_name_df.groupby('call_type')
['foul_called']
.mean()
.rename('avg_foul_called')
.reset_index()
)
.assign(diff=lambda df: df['foul_called'] - df['avg_foul_called']))The heatmaps below are broken out by call type, and show the difference between the foul call rate for each trailing/remaining possession combination and the overall foul call rate for the call type in question
def plot_foul_diff_heatmap(*_, data=None, **kwargs):
ax = plt.gca()
sns.heatmap(
data.pivot_table(
'diff',
'trailing_poss',
'remaining_poss'
),
cmap='seismic', robust=True,
cbar_kws={'format': pct_formatter}
)
ax.invert_yaxis()
ax.set_title("Observed foul call rate")
(sns.FacetGrid(diff_df, col='call_type', col_wrap=3, aspect=1.5)
.map_dataframe(plot_foul_diff_heatmap)
.set_axis_labels(
"Remaining possessions",
"Trailing possessions\n(committing team)"
)
.set_titles("{col_name}"));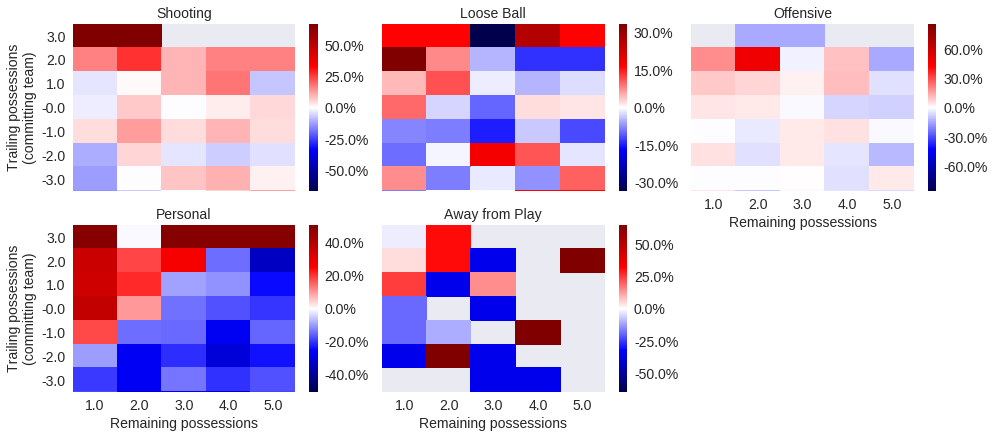
These plots confirm that most intentional fouls are personal fouls. They also show that the three-way interaction between trailing possesions, remaining possessions, and call type are important to model foul call rates.
\[ \begin{align*} \sigma_{\textrm{poss}, c} & \sim \operatorname{HalfNormal}(5) \\ \beta^{\textrm{poss}}_{t, r, c} & \sim \operatorname{Hierarchical-Normal}(0, \sigma_{\textrm{poss}, c}^2) \end{align*} \]
with poss_model:
β_poss = hierarchical_normal(
'β_poss',
(n_trailing_poss, n_remaining_poss, n_call_type),
σ_shape=(1, 1, n_call_type)
)The foul call rate is a combination of season, call type, and possession factors.
\[\eta^{\textrm{game}}_k = \beta^{\textrm{season}}_{s(k)} + \beta^{\textrm{call}}_{c(k)} + \beta^{\textrm{poss}}_{t(k),r(k),c(k)}\]
call_type = df['call_type'].valueswith poss_model:
η_game = β_season[season] \
+ β_call[call_type] \
+ β_poss[
trailing_poss,
remaining_poss,
call_type
]\[ \begin{align*} p_k & = \operatorname{sigm}\left(\eta^{\textrm{game}}_k\right) \end{align*} \]
with poss_model:
p = pm.Deterministic('p', pm.math.sigmoid(η_game))
y = pm.Bernoulli('y', p, observed=df['foul_called'])Infer the model given data
Again, we sample from the model’s posterior distribution.
with poss_model:
poss_trace = pm.sample(**SAMPLE_KWARGS)Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (3 chains in 3 jobs)
NUTS: [σ_β_poss_log__, Δ_β_poss, σ_β_call_log__, Δ_β_call, β_season]
100%|██████████| 1500/1500 [07:56<00:00, 3.15it/s]
There were 5 divergences after tuning. Increase `target_accept` or reparameterize.
There were 10 divergences after tuning. Increase `target_accept` or reparameterize.
There were 9 divergences after tuning. Increase `target_accept` or reparameterize.
The number of effective samples is smaller than 25% for some parameters.The BFMI and Gelman-Rubin statistics for this model indicate no problems with sampling and good convergence.
bfmi = pm.bfmi(poss_trace)
max_gr = max(
np.max(gr_stats) for gr_stats in pm.gelman_rubin(poss_trace).values()
)(pm.energyplot(poss_trace, legend=False, figsize=(6, 4))
.set_title(CONVERGENCE_TITLE()));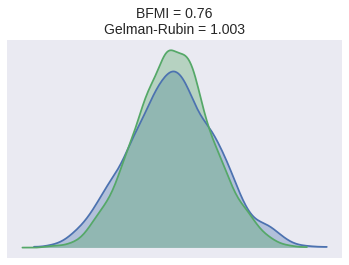
Criticize the model given data
Again, we calculate residuals.
resid_df = (df.assign(p_hat=poss_trace['p'].mean(axis=0))
.assign(resid=lambda df: df.foul_called - df.p_hat))The following plots show that, grouped various ways, the residuals for this model are relatively well-distributed.
ax = sns.heatmap(
resid_df.pivot_table(
'resid',
'trailing_poss',
'remaining_poss'
)
.rename_axis(
"Trailing possessions\n(committing team)",
axis=0
)
.rename_axis(
"Remaining possessions",
axis=1
)
.loc[-3:3],
cmap='seismic',
cbar_kws={'format': pct_formatter}
)
ax.invert_yaxis();
ax.set_title("Observed foul call rate");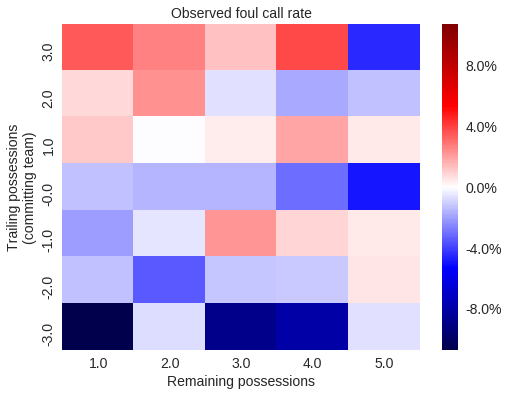
N_BIN = 20
bin_ix, bins = pd.qcut(
resid_df.p_hat, N_BIN,
labels=np.arange(N_BIN),
retbins=True
)ax = (resid_df.groupby(bins[bin_ix])
.resid.mean()
.rename_axis('p_hat', axis=0)
.reset_index()
.plot('p_hat', 'resid', kind='scatter'))
ax.xaxis.set_major_formatter(pct_formatter);
ax.set_xlabel(r"Binned $\hat{p}$");
make_foul_rate_yaxis(ax, label="Residual");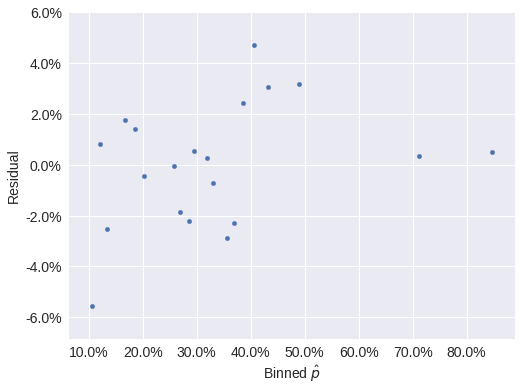
ax = (resid_df.groupby('seconds_left')
.resid.mean()
.reset_index()
.plot('seconds_left', 'resid', kind='scatter'))
make_time_axes(ax, ylabel="Residual");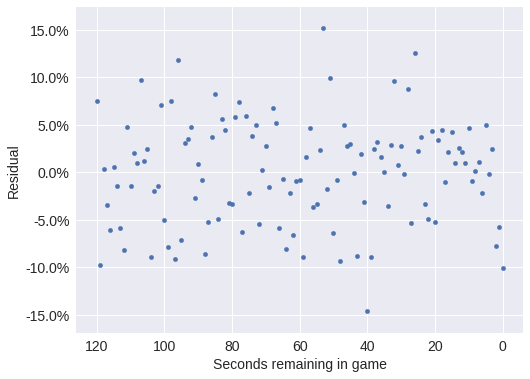
Model selection
Now that we have two models, we can engage in model selection. We use the widely applicable Bayesian information criterion (WAIC) for model selection.
MODEL_NAME_MAP = {
0: "Base",
1: "Possession"
}comp_df = (pm.compare(
(base_trace, poss_trace),
(base_model, poss_model)
)
.rename(index=MODEL_NAME_MAP)
.loc[MODEL_NAME_MAP.values()])Since smaller WAICs are better, the possession model clearly outperforms the base model.
comp_df| WAIC | pWAIC | dWAIC | weight | SE | dSE | var_warn | |
|---|---|---|---|---|---|---|---|
| Base | 11610.1 | 2.11 | 1541.98 | 0 | 56.9 | 73.43 | 0 |
| Possession | 10068.1 | 82.93 | 0 | 1 | 88.05 | 0 | 0 |
fig, ax = plt.subplots()
ax.errorbar(
np.arange(len(MODEL_NAME_MAP)),
comp_df.WAIC,
yerr=comp_df.SE, fmt='o'
);
ax.set_xticks(np.arange(len(MODEL_NAME_MAP)));
ax.set_xticklabels(comp_df.index);
ax.set_xlabel("Model");
ax.set_ylabel("WAIC");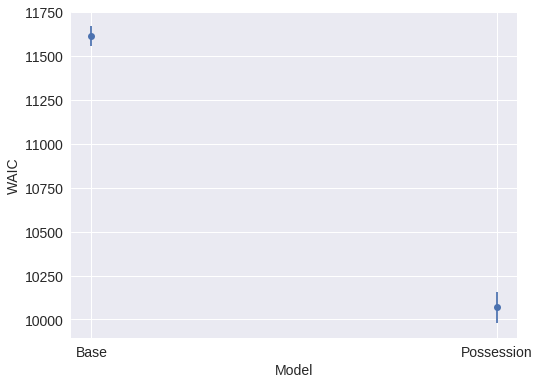
Player item-response theory model
Build a model of the science
We now turn to the question of whether or not committing and/or drawing fouls is a measurable skill. We use an item-response theory (IRT) model to study this question. For more information on Bayesian item-response models, consult the following references.
- Practical Issues in Implementing and Understanding Bayesian Ideal Point Estimation is an excellent introduction to applied Bayesian IRT models and has inspired much of this work.
- Bayesian Item Response Modeling — Theory and Applications is a comprehensive mathematical overview of Bayesien IRT modeling.
The item-response theory model includes the season, call type, and possession terms of the previous models.
with pm.Model() as irt_model:
β_season = pm.Normal('β_season', 0., 5., shape=n_season)
β_call = hierarchical_normal('β_call', n_call_type)
β_poss = hierarchical_normal(
'β_poss',
(n_trailing_poss, n_remaining_poss, n_call_type),
σ_shape=(1, 1, n_call_type)
)
η_game = β_season[season] \
+ β_call[call_type] \
+ β_poss[
trailing_poss,
remaining_poss,
call_type
]Each disadvantaged player has an ideal point (per season).
\[ \begin{align*} \sigma_{\theta} & \sim \operatorname{HalfNormal}(5) \\ \theta^{\textrm{player}}_{i, s} & \sim \operatorname{Hierarchical-Normal}(0, \sigma_{\theta}^2) \end{align*} \]
player_disadvantaged = df['player_disadvantaged'].values
n_player = player_enc.classes_.sizewith irt_model:
θ_player = hierarchical_normal(
'θ_player', (n_player, n_season)
)
θ = θ_player[player_disadvantaged, season]Each committing player has an ideal point (per season).
\[ \begin{align*} \sigma_{b} & \sim \operatorname{HalfNormal}(5) \\ b^{\textrm{player}}_{j, s} & \sim \operatorname{Hierarchical-Normal}(0, \sigma_{b}^2) \end{align*} \]
player_committing = df['player_committing'].valueswith irt_model:
b_player = hierarchical_normal(
'b_player', (n_player, n_season)
)
b = b_player[player_committing, season]Players affect the foul call rate through the difference in their ideal points.
\[\eta^{\textrm{player}}_k = \theta_k - b_k\]
with irt_model:
η_player = θ - bThe sum of the game and player effects determines the foul call probability.
\[\eta_k = \eta^{\textrm{game}}_k + \eta^{\textrm{player}}_k\]
with irt_model:
η = η_game + η_playerwith irt_model:
p = pm.Deterministic('p', pm.math.sigmoid(η))
y = pm.Bernoulli(
'y', p,
observed=df['foul_called']
)Infer the model given data
Again, we sample from the model’s posterior distribution.
with irt_model:
irt_trace = pm.sample(**SAMPLE_KWARGS)Auto-assigning NUTS sampler...
Initializing NUTS using jitter+adapt_diag...
Multiprocess sampling (3 chains in 3 jobs)
NUTS: [σ_b_player_log__, Δ_b_player, σ_θ_player_log__, Δ_θ_player, σ_β_poss_log__, Δ_β_poss, σ_β_call_log__, Δ_β_call, β_season]
100%|██████████| 1500/1500 [13:55<00:00, 1.80it/s]
There were 3 divergences after tuning. Increase `target_accept` or reparameterize.
There were 1 divergences after tuning. Increase `target_accept` or reparameterize.
There were 4 divergences after tuning. Increase `target_accept` or reparameterize.
The estimated number of effective samples is smaller than 200 for some parameters.None of the sampling diagnostics indicate problems with convergence.
bfmi = pm.bfmi(irt_trace)
max_gr = max(
np.max(gr_stats) for gr_stats in pm.gelman_rubin(irt_trace).values()
)(pm.energyplot(irt_trace, legend=False, figsize=(6, 4))
.set_title(CONVERGENCE_TITLE()));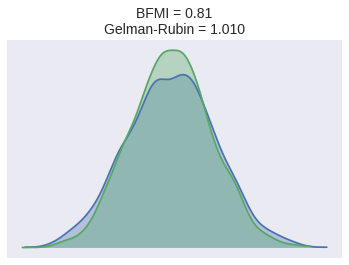
Criticize the model given data, take three
The binned residuals for this model are more asymmetric than for the previous models, but still not too bad.
resid_df = (df.assign(p_hat=irt_trace['p'].mean(axis=0))
.assign(resid=lambda df: df['foul_called'] - df['p_hat']))N_BIN = 50
bin_ix, bins = pd.qcut(
resid_df.p_hat, N_BIN,
labels=np.arange(N_BIN),
retbins=True
)ax = (resid_df.groupby(bins[bin_ix])
.resid.mean()
.rename_axis('p_hat', axis=0)
.reset_index()
.plot('p_hat', 'resid', kind='scatter'))
ax.xaxis.set_major_formatter(pct_formatter);
ax.set_xlabel(r"Binned $\hat{p}$");
make_foul_rate_yaxis(ax, label="Residual");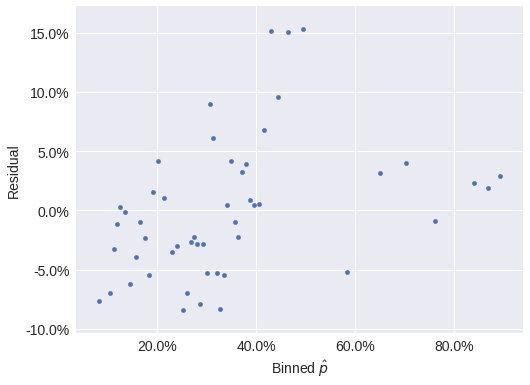
ax = (resid_df.groupby('seconds_left')
.resid.mean()
.reset_index()
.plot('seconds_left', 'resid', kind='scatter'))
make_time_axes(ax, ylabel="Residual");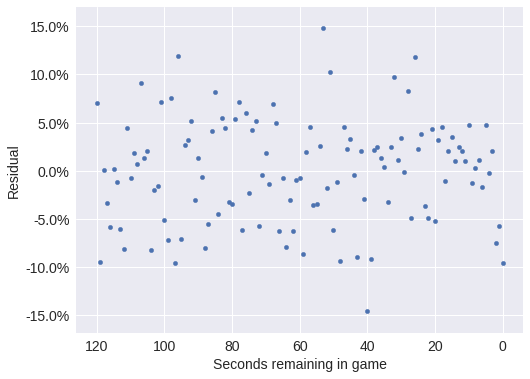
Model selection
The IRT model is a marginal improvement over the possession model in terms of WAIC.
MODEL_NAME_MAP[2] = "IRT"
comp_df = (pm.compare(
(base_trace, poss_trace, irt_trace),
(base_model, poss_model, irt_model)
)
.rename(index=MODEL_NAME_MAP)
.loc[MODEL_NAME_MAP.values()])comp_df| WAIC | pWAIC | dWAIC | weight | SE | dSE | var_warn | |
|---|---|---|---|---|---|---|---|
| Base | 11610.1 | 2.11 | 1566.92 | 0 | 56.9 | 74.03 | 0 |
| Possession | 10068.1 | 82.93 | 24.94 | 0.08 | 88.05 | 10.99 | 0 |
| IRT | 10043.2 | 216.6 | 0 | 0.91 | 88.47 | 0 | 0 |
fig, ax = plt.subplots()
ax.errorbar(
np.arange(len(MODEL_NAME_MAP)), comp_df.WAIC,
yerr=comp_df.SE, fmt='o'
);
ax.set_xticks(np.arange(len(MODEL_NAME_MAP)));
ax.set_xticklabels(comp_df.index);
ax.set_xlabel("Model");
ax.set_ylabel("WAIC");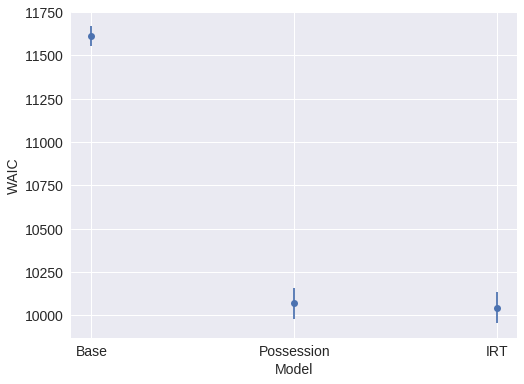
We now produce two DataFrames containing the estimated player ideal points per season.
def varname_to_param(varname):
return varname[0]
def varname_to_player(varname):
return int(varname[3:-2])
def varname_to_season(varname):
return int(varname[-1])irt_df = (pm.trace_to_dataframe(
irt_trace, varnames=['θ_player', 'b_player']
)
.rename(columns=lambda col: col.replace('_player', ''))
.T
.apply(
lambda s: pd.Series.describe(
s, percentiles=[0.055, 0.945]
),
axis=1
)
[['mean', '5.5%', '94.5%']]
.rename(columns={
'5.5%': 'low',
'94.5%': 'high'
})
.rename_axis('varname')
.reset_index()
.assign(
param=lambda df: df['varname'].apply(varname_to_param),
player=lambda df: df['varname'].apply(varname_to_player),
season=lambda df: df['varname'].apply(varname_to_season)
)
.drop('varname', axis=1))irt_df.head()| mean | low | high | param | player | season | |
|---|---|---|---|---|---|---|
| 0 | -0.016516 | -0.323127 | 0.272022 | θ | 0 | 0 |
| 1 | 0.003845 | -0.289842 | 0.290248 | θ | 0 | 1 |
| 2 | 0.008519 | -0.289715 | 0.304574 | θ | 1 | 0 |
| 3 | 0.031367 | -0.240853 | 0.339297 | θ | 1 | 1 |
| 4 | -0.037530 | -0.320010 | 0.226110 | θ | 2 | 0 |
player_irt_df = irt_df.pivot_table(
index='player',
columns=['param', 'season'],
values='mean'
)player_irt_df.head()| param | b | θ | ||
|---|---|---|---|---|
| season | 0 | 1 | 0 | 1 |
| player | ||||
| 0 | -0.069235 | 0.013339 | -0.016516 | 0.003845 |
| 1 | -0.003003 | 0.001853 | 0.008519 | 0.031367 |
| 2 | 0.084515 | 0.089058 | -0.037530 | -0.002373 |
| 3 | -0.028946 | 0.004360 | 0.003514 | -0.000334 |
| 4 | -0.001976 | 0.280380 | 0.072932 | 0.005571 |
The following plot shows that the committing skill appears to be somewhat larger than the disadvantaged skill. This difference seems reasonable because most fouls are committed by the player on defense; committing skill is quite likely to be correlated with defensive ability.
def plot_latent_params(df):
fig, ax = plt.subplots()
n, _ = df.shape
y = np.arange(n)
ax.errorbar(
df['mean'], y,
xerr=(df[['high', 'low']]
.sub(df['mean'], axis=0)
.abs()
.values.T),
fmt='o'
)
ax.set_yticks(y)
ax.set_yticklabels(
player_enc.inverse_transform(df.player)
)
ax.set_ylabel("Player")
return fig, ax
fig, axes = plt.subplots(
ncols=2, nrows=2, sharex=True,
figsize=(16, 8)
)
(θ0_ax, θ1_ax), (b0_ax, b1_ax) = axes
bins = np.linspace(
0.9 * irt_df['mean'].min(),
1.1 * irt_df['mean'].max(),
75
)
θ0_ax.hist(
player_irt_df['θ', 0],
bins=bins, normed=True
);
θ1_ax.hist(
player_irt_df['θ', 1],
bins=bins, normed=True
);
θ0_ax.set_yticks([]);
θ0_ax.set_title(
r"$\hat{\theta}$ (" + season_enc.inverse_transform(0) + ")"
);
θ1_ax.set_yticks([]);
θ1_ax.set_title(
r"$\hat{\theta}$ (" + season_enc.inverse_transform(1) + ")"
);
b0_ax.hist(
player_irt_df['b', 0],
bins=bins, normed=True, color=green
);
b1_ax.hist(
player_irt_df['b', 1],
bins=bins, normed=True, color=green
);
b0_ax.set_xlabel(
r"$\hat{b}$ (" + season_enc.inverse_transform(0) + ")"
);
b0_ax.invert_yaxis();
b0_ax.xaxis.tick_top();
b0_ax.set_yticks([]);
b1_ax.set_xlabel(
r"$\hat{b}$ (" + season_enc.inverse_transform(1) + ")"
);
b1_ax.invert_yaxis();
b1_ax.xaxis.tick_top();
b1_ax.set_yticks([]);
fig.suptitle("Disadvantaged skill", size=18);
fig.text(0.45, 0.02, "Committing skill", size=18)
fig.tight_layout();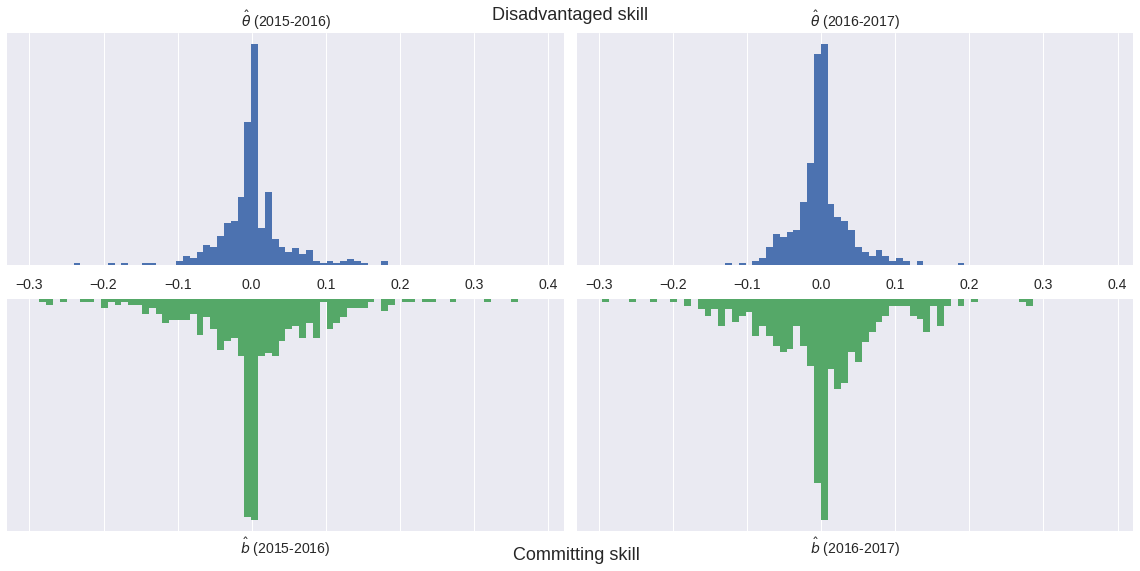
We now examine the top and bottom ten players in each ability, across both seasons.
The top players in terms of disadvantaged ability tend to be good scorers (Jimmy Butler, Ricky Rubio, John Wall, Andre Iguodala). The presence of DeAndre Jordan in the top ten may to be due to the hack-a-Shaq phenomenon. In future work, it would be interesting to control for the disavantage player’s free throw percentage in order to mitigate the influence of the hack-a-Shaq effect on the measurement of latent skill.
Interestingly, the bottom players (in terms of disadvantaged ability) include many stars (Pau Gasol, Carmelo Anthony, Kevin Durant, Kawhi Leonard). The presence of these stars in the bottom may somewhat counteract the pervasive narrative that referees favor stars in their foul calls.
top_bot_irt_df = (irt_df.groupby('param')
.apply(
lambda df: pd.concat((
df.nlargest(10, 'mean'),
df.nsmallest(10, 'mean')
),
axis=0, ignore_index=True
)
)
.reset_index(drop=True))top_bot_irt_df.head()| mean | low | high | param | player | season | |
|---|---|---|---|---|---|---|
| 0 | 0.351946 | -0.026786 | 0.762273 | b | 86 | 0 |
| 1 | 0.320737 | -0.027064 | 0.713128 | b | 23 | 0 |
| 2 | 0.280380 | -0.071020 | 0.695970 | b | 4 | 1 |
| 3 | 0.279678 | -0.057249 | 0.647667 | b | 462 | 1 |
| 4 | 0.271735 | -0.106795 | 0.676231 | b | 78 | 0 |
fig, ax = plot_latent_params(
top_bot_irt_df[top_bot_irt_df['param'] == 'θ']
.sort_values('mean')
)
ax.set_xlabel(r"$\hat{\theta}$");
ax.set_title("Top and bottom ten");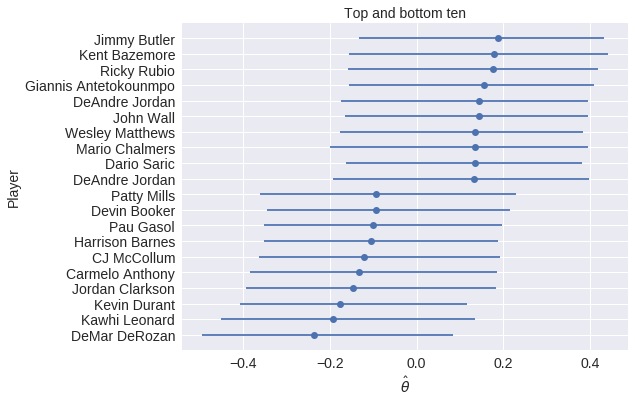
The top ten players in terms of committing skill include many defensive standouts (Danny Green — twice, Gordon Hayward, Paul George).
The bottom ten players include many that are known to be defensively challenged (Ricky Rubio and James Harden). Dwight Howard was, at one point, a fierce defender of the rim, but was well past his prime in 2015, when our data set begins. Chris Paul’s presence in the bottom is somewhat surprising.
fig, ax = plot_latent_params(
top_bot_irt_df[top_bot_irt_df['param'] == 'b']
.sort_values('mean')
)
ax.set_xlabel(r"$\hat{b}$");
ax.set_title("Top and bottom ten");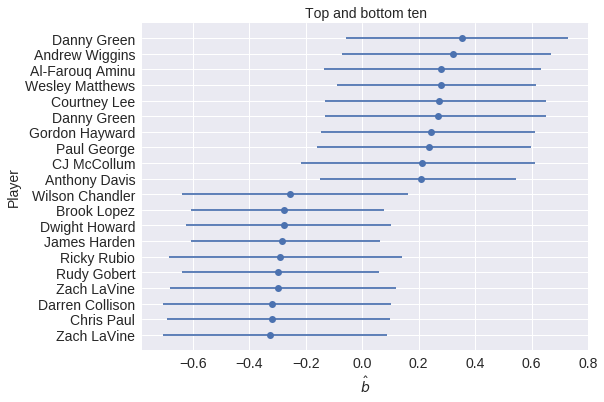
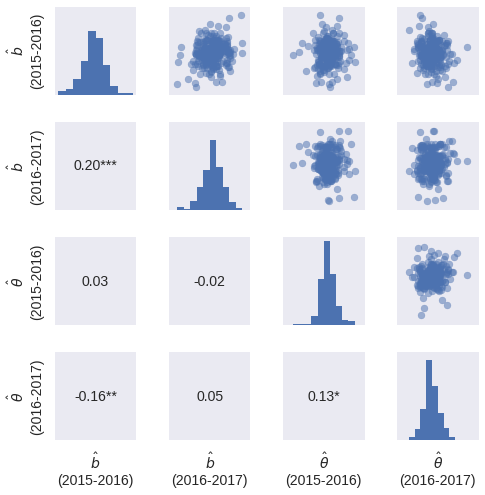
In the sports analytics community, year-over-year correlation of latent parameters is the test of whether or not a latent quantity truly measures a skill. The following plots show a slight year-over-year correlation in the committing skill, but not much correlation in the disadvantaged skill.
def p_val_to_asterisks(p_val):
if p_val < 0.0001:
return "****"
elif p_val < 0.001:
return "***"
elif p_val < 0.01:
return "**"
elif p_val < 0.05:
return "*"
else:
return ""
def plot_corr(x, y, **kwargs):
corrcoeff, p_val = sp.stats.pearsonr(x, y)
asterisks = p_val_to_asterisks(p_val)
artist = AnchoredText(
f'{corrcoeff:.2f}{asterisks}',
loc=10, frameon=False,
prop=dict(size=LABELSIZE)
)
plt.gca().add_artist(artist)
plt.grid(b=False)PARAM_MAP = {
'θ': r"$\hat{\theta}$",
'b': r"$\hat{b}$"
}
def replace_label(label):
param, season = eval(label)
return "{param}\n({season})".format(
param=PARAM_MAP[param],
season=season_enc.inverse_transform(season)
)
def style_grid(grid):
for ax in grid.axes.flat:
ax.grid(False)
ax.set_xticklabels([]);
ax.set_yticklabels([]);
if ax.get_xlabel():
ax.set_xlabel(replace_label(ax.get_xlabel()))
if ax.get_ylabel():
ax.set_ylabel(replace_label(ax.get_ylabel()))
return gridplayer_all_season = set(df.groupby('player_disadvantaged')
.filter(lambda df: df['season'].nunique() == n_season)
['player_committing']) \
& set(df.groupby('player_committing')
.filter(lambda df: df['season'].nunique() == n_season)
['player_committing'])style_grid(
sns.PairGrid(
player_irt_df.loc[player_all_season],
size=1.75
)
.map_upper(plt.scatter, alpha=0.5)
.map_diag(plt.hist)
.map_lower(plot_corr)
);
Since we can only reasonably estimate the skills of players for which we have sufficient foul call data, we plot the correlations below for players that appeared in at least ten plays in each season.
MIN = 10
player_has_min = set(df.groupby('player_disadvantaged')
.filter(lambda df: (df['season']
.value_counts()
.gt(MIN)
.all()))
['player_committing']) \
& set(df.groupby('player_committing')
.filter(lambda df: (df['season']
.value_counts()
.gt(MIN)
.all()))
['player_committing'])grid = style_grid(
sns.PairGrid(
player_irt_df.loc[player_has_min],
size=1.75
)
.map_upper(plt.scatter, alpha=0.5)
.map_diag(plt.hist)
.map_lower(plot_corr)
)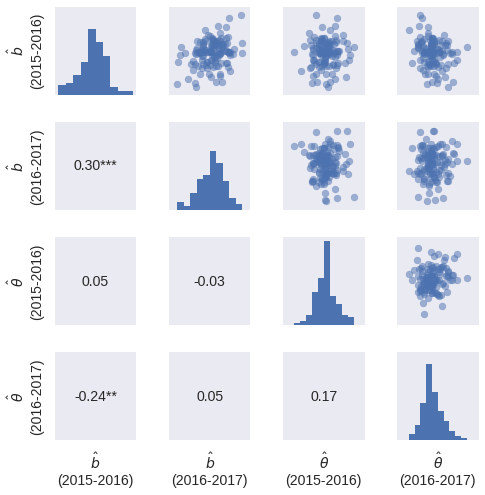
As expected, the season-over-season latent skill correlations are higher for this subset of players.
From this figure, it seems that committing skill (\(\hat{b}\)) exists and is measurable, but is fairly small. It also seems that disadvantaged skill (\(\hat{\theta}\)), if it exists, is difficult to measure from this data set. Ideally, the NBA would release a foul report for the entirety of every game, but that seems quite unlikely.
In the future it would be useful to include a correction for the probability that a given game appears in the data set. This correction would help with the sample bias introduced by the fact that only games that are close in the last two minutes are included in the NBA’s reports.
This post is available as a Jupyter notebook here.